Monitor
该题大意是给你一个 的矩阵, 同时还有p个小矩阵范围, 其中代表可以被保护的范围, 然后给q个小偷会偷的范围, 判断该范围是否存在没有被保护到的格子。
很难想对吧, 这就是属于难题的范畴了, 当然学会后收获的奖励----巧妙的思路也是很令人开心的咯。
首先肯定不能依次遍历然后判断每个格子能否被保护到, 这个算法效率太慢了, 数据范围是 这个数据范围有点奇怪, 也会带来一些奇怪的问题, 后面会说。但至少可以知道的是, 加上p个加保护操作, q个查询操作, 最大时间是远远超过 的。
既然普通方法不行, 那就想想之前有没有学过有关的, 也有, 是二维前缀和, 跟二维差分。可他们又不能帮你快速判断一个矩阵是否之前被完全保护过。不过这里矩阵的原始数据并没有给出, 诶那这就可以做点事情了。
从值入手, 如果想到这, 那就已经解开了该题的第一层面纱。怎么入手呢？假如全为0,代表都没保护, 紧接着显而易见的想法就是让值大于0的格子为受保护的格子, 好办, 用二维差分即可把区间中所有格子加上一个数。
那么判断一个区间是否被完全覆盖？emmm, 求一次二维前缀和后再根据矩形两个点来判断这个矩阵内的值总和是否大于0显然可以吧。当然, 这不可行。
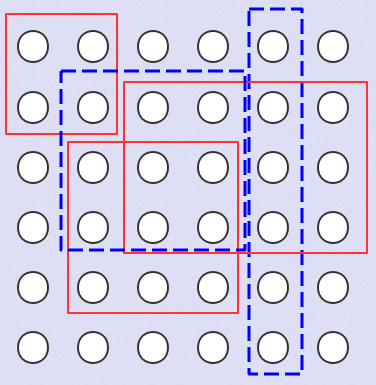如果按照之前的思路处理后, 对于数着的蓝框（即要查询的）, 因为经过了3个被保护的格子, 其6个格子总和还是大于0的, 那么会输出被完全保护, 但里面有3个没被保护, 因此该方法不可以。
那有没有方法可以让没保护到的格子影响到最终求和的结果呢？或者说, 让最终求和结果能够反应出是否需被完全覆盖。我们可以假设被保护的格子其值为1, 那么对于一个矩形保护区间, 其区间和就是面积。
也就是说, 当设定所有被保护的格子值都为1时, 就具有矩形求和值为其面积值这个性质。
所以具体操作就是先差分, 前缀和应用变化, 然后把所有值大于等于1的格子的值设为1。最后求一次前缀和, 然后判断区间的和是否等于这个区间的面积即可。如果等于说明就全部被1覆盖, 没有少的。
而题目的nm范围, 导致不能使用一般的二维表示法sum[N][M], 会内存超限, 这里就得化一维矩阵：
假设有 n 行，m列的矩阵
二维表示法：sum[i][j]
一维表示法：sum[ (i - 1) * m + j ]
也可以用vector动态数组来解决。
#include <cstdio>
#include <cstring>
const int N = 1e7+10;
long long sum[N]; // 二维转一维
int n, m;
void add_1(int x, int y, int c)
{
if (x > n || y > m) return;
sum[((x - 1) * m) + y] += c;
}
void add(int x1, int y1, int x2, int y2,int c) // 差分构建
{
add_1(x1, y1, c);
add_1(x1, y2 + 1, -c);
add_1(x2 + 1, y1, -c);
add_1(x2 + 1, y2 + 1, c);
}
int query(int x, int y)
{
if (x == 0 || y == 0)
return 0;
return sum[(x - 1) * m + y];
}
void getsum() // 求一次前缀和
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
sum[(i - 1) * m + j] = query(i - 1, j) + query(i, j - 1) - query(i - 1, j - 1) + query(i, j);
}
}
}
int main()
{
while (scanf("%d%d", &n, &m) != EOF)
{
memset(sum, 0, sizeof(sum));
//m += 1;
// 开始标记两点
int q;
scanf("%d", &q);
while (q--)
{
int x1, x2, y1, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
add(x1, y1, x2, y2, 1);
}
getsum(); // 求标记数组
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (query(i, j) > 1) sum[(i - 1) * m + j] = 1;
getsum();
int p;
scanf("%d", &p);
while (p--)
{
int x1, x2, y1, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
long long temp = query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1);
long long S = (x2 - x1 + 1) * (y2 - y1 + 1);
if (temp == S) printf("YES\n");
else printf("NO\n");
}
}
return 0;
}