有向无环图上的动态规划是学习动态规划的基础, 很多问题都可以转化为DAG上最长路, 最短路或路径计数问题。

9.2.1 DAG模型

9.2.2嵌套矩形问题

有n个矩形，每个矩形可以用两个整数a、b描述，表示它的长和宽。矩形X(a,b)可以嵌套在矩形Y(c, d)中，当且仅当a＜c，b＜d，或者b＜c，a＜d（相当于把矩形X旋转90°）。例如，(1, 5)可以嵌套在(6, 2)内，但不能嵌套在(3, 4)内。你的任务是选出尽量多的矩形排成一行，使得除了最后一个之外，每一个矩形都可以嵌在下一个矩形内。如果有多解，矩形编号的字典序应尽量小。

可嵌套是一个典型二元关系, 可以在图上连个边A→B代表A可以镶嵌到B里, 该图是无环的, 因为矩形不能自己镶嵌自己里面, 该题就是DAG上的最长路模型。

以 i 为结尾

设f[i] 为以点i为结尾的最长路, 我们需要枚举所有能到i的点并更新。 状态计算： f[i] = max(f[i], f[j] + 1) 因为DAG图中f[j] 不一定已经被更新, 所以这里使用记忆化搜索来做 f[i] = max(f[i], dp(j) + 1)

int dp(int u)
{
	int &ans = f[u];
	if(ans != -1) return ans;
	ans = 1;
	for(int i = 1; i <= n; i++)
	{
		if(g[i][u])
			ans = max(ans, dp(i) + 1);
	}
	return ans;
}

这里用到了一个技巧：为表项d[i]声明一个引用ans。这样，任何对ans的读写实际上都是在对d[i]进行。当d[i]换成d[i][j][k][l][m][n]这样很长的名字时，该技巧的优势就会很明显。

打印方案的方法是先获得最大数量dp[i]对应的i, 然后根据转移方程 dp[i] = max{dp[j] + 1} 得出, 当 dp[i] == dp[j] + 1 时, j就是下一个矩阵。

void print_ans(int i)
{
	// cout << i << " "; 放到这里会是逆序输出 
	for(int j = 1; j <= n; j++)
		if(g[j][i] && dp[i] == dp[j] + 1) // 如果j可以镶嵌到i里面
		{
			print_ans(j);
			break;
		}
	cout << i << " ";
}

打印全部方案时, 用栈来存当前路径

void print_all_ans(int i, int head) // i是以第i个为结尾的矩阵, head是该路径的头（最大的那个矩阵,也是i）
{
	int flag = true;
	for(int j = 1; j <= n; j++)
	{
		if(g[i][j] && dp[i] == dp[j] + 1)
		{
			stk[top++] = j;
			print_all_ans(j, head);
			top--;
			flag = false; // 存在j可以镶嵌在i里面, 说明路径未结束
		}
	}
	if(flag) // 路径截止, 输出路径
	{
		for(int i = 0; i < top; i++) cout << stk[i] << " ";
		cout << head << endl;
	}
}

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
 
int readInt()
{
    int t;
    cin >> t;
    return t;
}
 
//------- Coding Area ---------//
const int N = 1e3 + 10, M = 2 * N;
int g[N][N],stk[N],top;
int n;
int f[N];
typedef struct Rect
{
    int x, y;
    bool operator<(const Rect w) const
    {
        if ((x < w.x && y < w.y) || (y < w.x && x < w.y))
            return true;
        return false;
    }
} Rect;
Rect a[N];
 
int dp(int u)
void print_ans(int i)
void print_all_ans(int i, int head)
 
 
int main()
{
    int T;
    cin >> T;
    while (T--)
    {
        cin >> n;
        mem(f, -1);
        mem(g,0);
        for (int i = 1; i <= n; i++)
        {
            cin >> a[i].x >> a[i].y;
           for(int j = 1; j < i; j++)
           {
               if(a[i] < a[j])
                    g[i][j] = 1;
               else if(a[j] < a[i])
                    g[j][i] = 1;
           }
        }
            
        int res = 1, num = 0;
        for (int i = 1; i <= n; i++)
            if(res < dp(i))
            {
                res = f[i];
                num = i;
            }
        cout << res << endl;
        for(int i = 1; i <= n; i++)
            if(res == f[i])
                print_all_ans(i, i);
        //print_ans(num);
    }
    return 0;
}

以 i 为开始

建图是一样的, 循环计算时得变一变 状态表示： f[i] 以 i 矩阵为开始的最长矩阵镶嵌数量 状态计算： f[i] = max(f[i], f[j] + 1) 如果i能镶嵌到j里, 那么结果就是以 j 开始的最长串前面加 1

int dp(int i)
{
	int &ans = f[i];
	if(ans != -1)  return ans;
	ans = 1;
	for(int j = 1;j <= n; j++)
		if(g[i][j])
			ans = max(ans, dp(j) + 1);
	return ans;
}

打印路径：

void print_ans(int i)
{
	cout << i << " ";
	for(int j = 1; j <= n; j++)
		if(g[i][j] && f[i] == f[j] + 1)
		{
			print_ans(j);
			break;
		}
}

打印所有路径:

void print_all_ans(int i)
{
	int flag = true;
	for(int j = 1; j <= n; j++)
	{
		if(g[i][j] && f[i] == f[j] + 1)
		{
            stk[top++] = j;
			print_all_ans(j);
            top--;
			flag = false;
		}
	}
	if(flag)
    {
        for(int i = 0; i < top; i++) cout << stk[i] << " ";
        cout << endl;
    }
}

为何以i为结尾时不能是字典序

以i为结尾时, 显然是以结尾的顺序, 而题目要求的是以小的开始。观察一下第一个输出可以发现, 8之前一位数是以正序排列, 而第二个输出则是乱序。所以以正序输出时不会是字典序。

9.2.3硬币问题

有n种硬币，面值分别为 $V_{1}, V_{2}, \dots, V_{n}$ ，每种都有无限多。给定非负整数S，可以选用多少个硬币，使得面值之和恰好为 $S$ ？输出硬币数目的最小值和最大值。 $1 \leq n \leq 100 ， 0 \leq S \leq 10000 ， 1 \leq V_{i} \leq S$ 。

是完全背包问题, 书上用DAG图来解释, 初始状态为S, 目标状态为0, 每用一个硬币j, 就将状态转移到i - j, 矩形嵌套是无固定起点终点的最长路, 这里是固定起点终点的最长路最短路。

状态表示： f[i] 面值之和为i的硬币个数 状态计算： f[i] = max(f[i], dp(i - Vj) + 1) Vj是第j种硬币的面值

因为S可以为0, 故状态初始化时不能用0来表示还未枚举到, 需用-1来标识。且有可能无法到达S, 故还需用 -(1 << 30) 来标识是否可以到达。

也可以用空间换可读性, 用vis数组来表示是否访问过, 代替-1。

当程序中需要用到特殊值时，应确保该值在正常情况下不会被取到。这不仅意味着特殊值不能有“正常的理解方式”，而且也不能在正常运算中“意外得到”。递归写法：

int dp(int S)
{
	int &ans = d[S];
	if(ans != -1) return ans;
	ans = -(1 << 30);
	for(int i = 1; i <= n; i++) ans = max(ans, dp(S - v[i]) + 1);
	return ans;
}

递推写法：

minv[0] = maxv[0] = 0;
for(int i = 1; i <= S; i++)
	minv[i] = INF, maxv[i] = -INF;
for(int i = 1; i <= S; i++)
{
	for(int j = 1; j <= n; j++)
	{
		if(i >= v[j])
		{
			minv[i] = min(minv[i], minv[i - v[j]] + 1);
			maxv[i] = max(maxv[i], maxv[i - v[j]] + 1);
		}
	}
}
cout << maxv[S] << " " << minv[S] << endl;

打印结果：

void print_ans(int *d, int S) // 第一个是传入哪个数组
{
	for(int i = 1; i <= n; i++)
		if(S >= v[i] && d[S] == d[S - v[i]] + 1)
		{
			cout << i << " ";
			print_ans(d, S - v[i]);
			break;
		}
}

用指针传递数组时不会复制数组内元素, 不必担心带来不必要的时间开销。

可以优化掉print里面的循环, 用 min_coin/max_coin 来记录满足minv[S] == min[S - v[i]] + 1 的最小 i。

if(maxv[i] < maxv[i - v[j]] + 1)
{
	maxv[i] = maxv[i - v[j]] + 1;
	max_coin[i] = j;
}
if(minv[i] > minv[i - v[j]] + 1)
{
	minv[i] = minv[i - v[j]] + 1;
	min_coin[i] = j;
}
 
// 输出
void print_ans(int *d, int S)
{
	while(S)
	{
		cout << d[S] << " ";
		S -= v[d[S]];
	}
}
 
// 调用
print_ans(max_coin, S);
print_ans(min_coin, S);

传统的递推法可以表示成“对于每个状态i，计算f(i)”，或者称为“填表法”。这需要对于每个状态i，找到f(i)依赖的所有状态，在某些时候并不方便。另一种方法是“对于每个状态i，更新f(i)所影响到的状态”，或者称为“刷表法”，有时比填表法方便。但需要注意的是，只有当每个状态所依赖的状态对它的影响相互独立时才能用刷表法。

例题

例题9-1 城市里的间谍（A Spy in the Metro, ACM/ICPC World Finals 2003,UVa1025）

A Spy in the Metro - UVA 1025 - Virtual Judge (csgrandeur.cn) 某城市地铁是一条直线，有 n（2 ≤ n ≤ 50）个车站，从左到右编号 1 … n。有 M1 辆列车从第 1 站开始往右开，还有 M2 辆列车从第 n 站开始往左开。列车在相邻站台间所需的运行时间是固定的，因为所有列车的运行速度是相同的。在时刻 0，Mario 从第 1 站出发，目的在时刻 T（0 ≤ T ≤ 200）会见车站 n 的一个间谍。在车站等车时容易被抓，所以她决定尽量躲在开动的火车上，让在车站等待的时间尽量短。列车靠站停车时间忽略不计，且 Mario 身手敏捷，即时两辆方向不同的列车在同一时间靠站，Mario 也能完成换乘。

输入格式输入文件包含多组数据。

每一组数据包含以下 7 行：第一行是一个正整数 n，表示有 n 个车站。第二行是为 T，表示 Mario 在时刻 T 会见车站 n 的间谍。第三行有 n−1 个整数 t1, t2, … , tn-1 ,其中 ti表示地铁从车站 i 到 i+1 的行驶时间。第四行为 M1，及从第一站出发向右开的列车数目。第五行包含 M1 个正整数 a1,a2,…,a M1，即每个列车出发的时间。第六行为 M2，即从第 n 站出发向左开的列车数目。第七行包含 M2 个正整数 b1,b2, … , b M2，即每个列车出发的时间。输入文件以一行 0 结尾。

输出格式有若干行，每行先输出 Case Number XXX :（XXX为情况编号，从 1 开始），再输出最少等待时间或 impossible（无解）。

input

4
55
5 10 15
4
0 5 10 20
4
0 5 10 15
4
18
1 2 3
5
0 3 6 10 12
6
0 3 5 7 12 15
2
30
20
1
20
7
1 3 5 7 11 13 17
0

output

Case Number 1: 5
Case Number 2: 0
Case Number 3: impossible

思路

时间是单向流逝的，是一个天然的“序”。影响到决策的只有当前时间和所处的车站，所以可以用d(i,j)表示时刻i，你在车站j（编号为1～n），最少还需要等待多长时间。边界条件是d(T,n)=0，其他d(T,i)（i不等于n）为正无穷

有如下3种决策决策1：等1分钟决策2：搭乘往右开的车（如果有）决策3：搭乘往左开的车（如果有）主过程的代码如下：

代码

#include <iostream>
#include <cstring>
#include <string>
using namespace std;
const int N = 55, T = 220, INF = 0x3f3f3f3f;
bool has_train[T][N][2];
int f[T][N]; // 在时刻i, 车站j时需要等的时间
int t[N];
// 决策： 1等待一分钟 2向左的火车 3向右的火车
 
 
int main()
{
	int n,m, ti, kase = 0;
	while(cin >> n && n)
	{
		memset(f,0,sizeof f);
		memset(has_train, false, sizeof has_train);
		cin  >> m;
		for(int i = 1; i < n;i ++) cin >> t[i];
		cin >> ti;
		while(ti--)
		{
			int time, sta = 1;
			cin >> time;
			while(time <= m && sta < n)
			{
				has_train[time][sta][1] = 1;
				time += t[sta];
				sta += 1;
			}
		}
		cin >> ti;
		while(ti--)
		{
			int time, sta = n;
			cin >> time;
			while(time <= m && sta > 0)
			{
				has_train[time][sta][0] = 1;
				time += t[sta - 1];
				sta -= 1;
			}
		}
		
		for(int i = 1; i <= n; i++) f[m][i] = INF;
		f[m][n] = 0;
		for(int j = m - 1; j >= 0; j--)
		{
			for(int i = 1; i <= n; i++)
			{
				f[j][i] = f[j + 1][i] + 1;
				if(i < n && has_train[j][i][1] && j + t[i] <= m)
					f[j][i] = min(f[j][i], f[j + t[i]][i + 1]);
				if(i > 1 && has_train[j][i][0] && j + t[i - 1] <= m)
					f[j][i] = min(f[j][i], f[j + t[i - 1]][i - 1]);
			}
		}
		cout << "Case Number " << ++kase << ": ";
		if(f[0][1] >= INF)
			cout << "impossible\n";
		else cout << f[0][1] << endl;
	}
	return 0;
}

例题9-2 巴比伦塔（The Tower of Babylon, UVa 437）

你可能已经听说过巴比伦塔的传说。现在这个传说的许多细节已经被遗忘。所以本着本场比赛的教育性质，我们现在会告诉你整个传说：

巴比伦人有n种长方形方块，每种有无限个，第i种方块的三边边长是xi,yi,zi。对于每一个方块，你可以任意选择一面作为底，这样高就随着确定了。举个例子，同一种方块，可能其中一个是竖着放的，一个是侧着放的，一个是横着放的。

他们想要用堆方块的方式建尽可能高的塔。问题是，只有一个方块的底的两条边严格小于另一个方块的底的两条边，这个方块才能堆在另一个上面。这意味着，一个方块甚至不能堆在一个底的尺寸与它一样的方块的上面。

你的任务是编写一个程序，计算出这个塔可以建出的最高的高度。

【输入格式】

输入会包含至少一组数据，每组数据的第一行是一个整数n(n⇐30)，表示方块的种类数。这组数据接下来的n行，每行有三个整数，表示xi,yi,zi。输入数据会以0结束。

【输出格式】

对于每组数据，输出一行，其中包含组号(从1开始)和塔最高的高度。按以下格式： Case : maximum height = __

思路

和9 2 2嵌套矩形问题很像, 不过可以旋转长方形, 这里则用类似于9-1 题的思路, 将长方体每次旋转后得到的底面作为矩形存入, 其高就是权值。

状态表示： f[i] 从第i个矩阵开始嵌套的最长高度 状态计算： f[i] = max(f[i], f[j] + w[i]) if g[i][j] g[i][j] 仍然表示矩形i是否能镶嵌到j里。

代码

const int N = 200;
struct Rect
{
    int x, y, w;
    bool operator<(const Rect &w)
    {
        if (w.x > x && w.y > y)
            return true;
        return false;
    }
} t[N];
bool g[N][N];
int f[N];
int cnt = 0;
 
int dp(int i)
{
    if (f[i] != -1)
        return f[i];
    f[i] = t[i].w;
    for (int j = 1; j <= cnt; j++)
    {
        if (g[i][j])
            f[i] = max(f[i], dp(j) + t[i].w);
    }
    return f[i];
}
 
int main()
{
    int n, kase = 0;
    while (cin >> n && n)
    {
        cnt = 0;
        memset(g, false, sizeof g);
        memset(t, 0, sizeof t);
        memset(f, -1, sizeof f);
        while (n--)
        {
            int x, y, z;
            cin >> x >> y >> z;
            t[++cnt] = {x, y, z};
            t[++cnt] = {x, z, y};
            t[++cnt] = {y, x, z};
            t[++cnt] = {y, z, x};
            t[++cnt] = {z, x, y};
            t[++cnt] = {z, y, x};
        }
        for (int i = 1; i <= cnt; i++)
        {
            for (int j = 1; j <= cnt; j++)
            {
                if (t[i] < t[j])
                    g[i][j] = true;
                else if (t[j] < t[i])
                    g[j][i] = true;
            }
        }
        int res = 0;
        /*
        for (int k = 1; k <= cnt; k++)
 
            for (int i = cnt; i >= 1; i--)
            {
                if (!f[i])
                    f[i] = t[i].w;
                for (int j = cnt; j >= 1; j--)
                {
                    if (g[i][j])
                        f[i] = max(f[i], f[j] + t[i].w);
                }
                res = max(f[i], res);
            }
        */
        for (int i = 1; i <= cnt; i++)
            res = max(res, dp(i));
        cout << "Case " << ++kase << ": maximum height = " << res << endl;
    }
 
    return 0;
}

例题9-3 旅行（Tour, ACM/ICPC SEERC 2005, UVa1347）

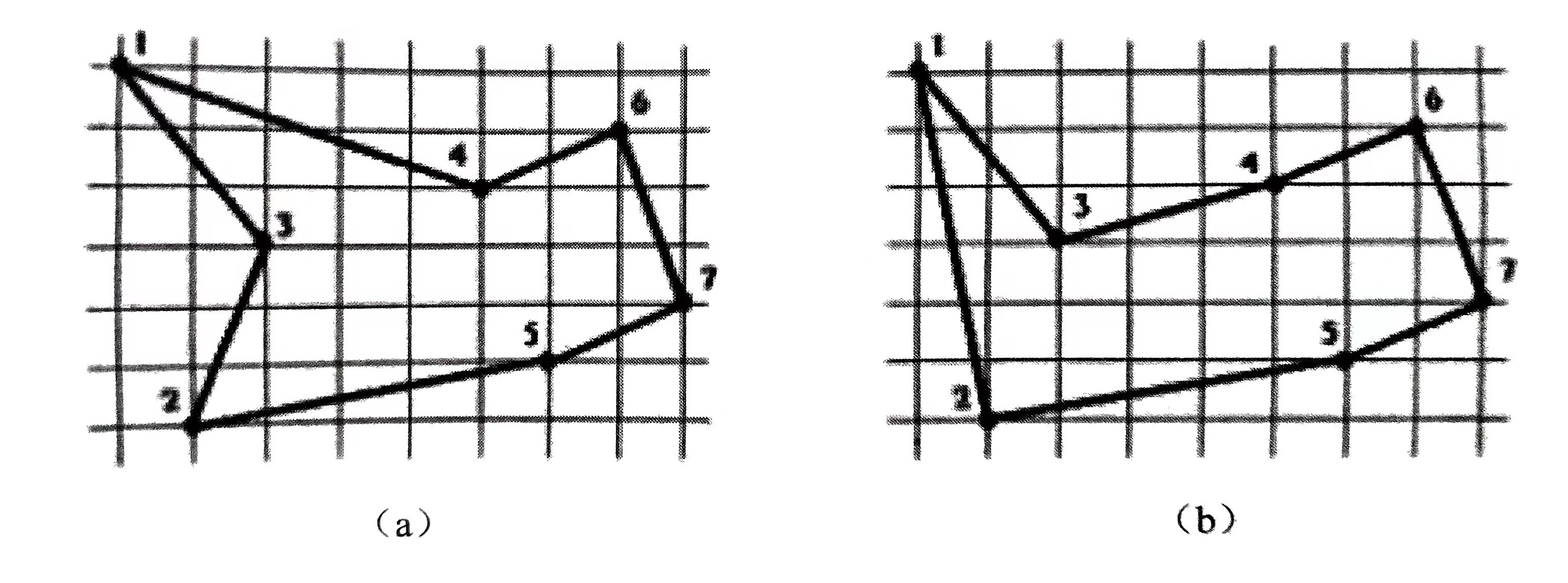
给定平面上 n(n≤1000) 个点的坐标(按照x递增的顺序给出。各点x坐标不同，且均为正整数)，你的任务是设计一条路线，从最左边的点出发，走到最右边的点后再返回，要求除了最左点和最右点之外每个点恰好经过一次，且路径总长度最短。两点间的长度为它们的欧几里德距离，如图所示

数据按x坐标升序给出每组样例输出一个带有两位小数的浮点数表示最短长度

input

output

6.47
7.89

思路

可以从任何一点出发到达其他任何一个点。直接用 O(n^2) 建图, 然后以最后一个点为终点和起点做两次dijkstra

不能用dijksta, 他要求遍历所有点。

“从左到右再回来”不太方便思考，可以改成：两个人同时从最左点出发，沿着两条不同的路径走，最后都走到最右点，且除了起点和终点外其余每个点恰好被一个人经过。这样，就可以用d(i,j)表示第一个人走到i，第二个人走到j，还需要走多长的距离。

状态如何转移呢？仔细思考后会发现：好像很难保证两个人不会走到相同的点。例如，计算状态d(i,j)时，能不能让i走到i＋1呢？不知道，因为从状态里看不出来i＋1有没有被j走过。换句话说，状态定义得不好，导致转移困难。

换一种定义方法：d[i][j] 表示 1~max(i,j) 都走过, 且两人当前位置为 i, j 时, 还要走多长的距离。显然 d[i][j] == d[j][i] 俩人谁走都行。故这里可以令 i > j 避免重复计算。这样下一步就只能走 i+1, i+2, i+3,... 这些点, 但走到 i+2 时会发现 i+1 没走过, 跟状态定义相违背, 于是禁止这么走, 只能走i+1。这样规定是否会出现漏解？并不会, 若第一个人走到了 i+1 , 那么第二个人只能走到 i+2, 此时也相当于第一个人走到了i+2, 其他同理。

状态表示： f[i][j] 前 1~max(i,j) 都走过, 当前俩人位置为i,j时, 还要走的距离的最小值 状态计算： f[i][j] = min(f[i + 1][j] + g[i][i + 1], f[i + 1][i] + g[j][i + 1]) 边界条件f[n - 1][j] = g[n-1][n] + g[j][n]

解释几个问题：

为啥这里只有 f[i+1][j] 和 f[i+1][i], 而不是 f[i+1][j] 和f[i][j+1] ? f[i+1][j] 很好理解, 是 i 代表的人走到 i+1点上而 f[i+1][i] 表示 j 代表的人走到 i+1 点上, 此时因为需要要求 i>j 故将他俩交换一下。不用f[i][j+1] 是因为 j 无法走到 j+1, 根据状态定义, 1~max(i,j) 都已经走过, 显然这里 i 比 j 大, 故 j 代表的人只能走 i+1
边界条件为什么这么设计？理解了上一个问题之后这个就显而易见了, 到达 max(n-1, j) 状态时, 第一个人走到n代表第一次到达, 第二个人走到n 代表第二次到达, 相加就是来回的值。
为什么i层循环要逆序且最小为2？逆序因为要用到 i + 1, 最小为 2 因为要保证 i>j , 且不存在f[1][1]的状态
为什么结果输出 dist[2][1] + g[1][2] 此时 dist[2][1] 的值就是i在点2, j在点1, 此时两人还没有汇合, 加上俩人的距离即是最终结果。

代码

const int N = 1e3 + 10, M = N * 4;
int h[N], e[M], ne[M], idx;
double dist[N][N];
double g[N][N];
bool st[N];
int n, m;
struct Point
{
    double x, y;
} p[N];
 
double getdistance(Point a, Point b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
 
int main()
{
    setPrec(2);
    while (cin >> n)
    {
 
        for (int i = 1; i <= n; i++)
        {
            double x, y;
            cin >> x >> y;
            p[i] = {x, y};
            for (int j = 1; j < i; j++)
                g[i][j] = g[j][i] = getdistance(p[i], p[j]);
        }
        mem(dist, 0x3f);
        for (int i = n - 1; i >= 2; i--)
        {
            for (int j = 1; j < i; j++)
            {
                if (i == n - 1)
                    dist[i][j] = g[i][n] + g[j][n];
                else
                    dist[i][j] = min(dist[i + 1][j] + g[i][i + 1], dist[i + 1][i] + g[j][i + 1]);
            }
        }
        cout << g[1][2] + dist[2][1] << endl;
    }
 
    return 0;
}

🪴 Edwin Aze's Blog

最近文章

洛师薅羊毛教程

挖土机编程 CSP-J 2022 模拟赛 Round 2

我是学生如何白嫖GPT4

最近笔记

Hi~

202503051617 latex documentclass options

9.2 DAG上的动态规划

9.2.1 DAG模型

9.2.2嵌套矩形问题

以 i 为结尾

以 i 为开始

为何以i为结尾时不能是字典序

9.2.3硬币问题

例题

例题9-1 城市里的间谍（A Spy in the Metro, ACM/ICPC World Finals 2003,UVa1025）

思路

代码

例题9-2 巴比伦塔（The Tower of Babylon, UVa 437）

思路

代码

例题9-3 旅行（Tour, ACM/ICPC SEERC 2005, UVa1347）

思路

代码

目录

🪴 Edwin Aze's Blog

最近文章

洛师薅羊毛教程

挖土机编程 CSP-J 2022 模拟赛 Round 2

我是学生 如何白嫖GPT4

最近笔记

Hi~

202503051617 latex documentclass options

9.2 DAG上的动态规划

9.2.1 DAG模型

9.2.2嵌套矩形问题

以 i 为结尾

以 i 为开始

为何 以i为结尾时 不能是字典序

9.2.3硬币问题

例题

例题9-1 城市里的间谍（A Spy in the Metro, ACM/ICPC World Finals 2003,UVa1025）

思路

代码

例题9-2 巴比伦塔（The Tower of Babylon, UVa 437）

思路

代码

例题9-3 旅行（Tour, ACM/ICPC SEERC 2005, UVa1347）

思路

代码

目录

我是学生如何白嫖GPT4

为何以i为结尾时不能是字典序