🪴 Edwin Aze's Blog

最近文章

最近笔记

最长上升子序列问题LST

15分钟阅读

拦截导弹

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式

一行，若干个整数，中间由空格隔开。

输出格式

两行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

样例 #1

样例输入 #1

389 207 155 300 299 170 158 65

样例输出 #1

6
2

P1020 [NOIP1999 普及组] 导弹拦截 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 对于任何一个导弹, 拦截之后它必然是一个子序列的结尾。

需要考虑两种选择： 接在现有的某个子序列之后 创建一个新的子序列

对于每个序列的结尾数一定是越大越好, 利于后面的拦截 故选择导弹所接的序列时一定是前面最小的大于等于该导弹高度

贪心证明：

  1. 证明两数相等 A>=B, B⇐A
  2. 调整法 若贪心解与最优解不同, 但两者可以交换, 则贪心解就是最优解
  3. 反证法

一个序列用多少个非上升子序列覆盖掉, 等于一个序列的最长上升子序列长度

若数组升序排列 lower_bound(begin, end, a) 返回数组[begin, end)之间第一个大于或等于a的地址，找不到返回end （可以等于所以low） upper_bound(begin, end, a) 返回数组[begin, end)之间第一个大于a的地址，找不到返回end （一定大于所以up）

若数组降序排列，可写上比较函数greater<type>() lower_bound(begin, end, a, greater<int>()) 返回数组[begin, end)之间第一个小于或等于a的地址，找不到返回end upper_bound(begin, end, a, greater<int>()) 返回数组[begin, end)之间第一个小于a的地址，找不到返回end

代码

 const int N = 1e5 + 10;
int a[N];
int f[N], g[N];
 
int main()
{
    int t, n = 0;
    int cnt1 = 0, cnt2 = 0;
    while (cin >> t && t)
    {// 最长下降子序列
        int pos1 = upper_bound(f, f + cnt1, t, greater<int>()) - f;
        if (pos1 == cnt1)
            f[cnt1++] = t;
        else
            f[pos1] = t;
// 最长上升子序列
        int pos2 = lower_bound(g, g + cnt2, t) - g;
        if (pos2 == cnt2)
            g[cnt2++] = t;
        else
            g[pos2] = t;
    }
    cout << cnt1 << endl;
    cout << cnt2 << endl;
    return 0;
}

友好城市

题目描述

有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航道不相交的情况下，被批准的申请尽量多。

输入格式

第1行，一个整数N，表示城市数。

第2行到第n+1行，每行两个整数，中间用一个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。

输出格式

仅一行，输出一个整数，表示政府所能批准的最多申请数。

样例 #1

样例输入 #1

7
22 4
2 6
10 3
15 12
9 8
17 17
4 2

样例输出 #1

4

提示

50% 1⇐N⇐5000,0⇐xi⇐10000

100% 1⇐N⇐2e5,0⇐xi⇐1e6

思路

条件1：每个城市上只能建立一座桥 条件2：所有桥与桥之间不能相交 目标：最多可以建多少桥？

先将一侧排序, 排序后的问题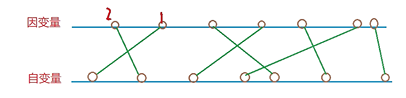： 下面是排好序的, 此时随便选择一些 合法的建桥方式, 会发现所对应于因变量的都是上升子序列, 而非上升子序列一定是不合法的, 所以就可以得出：

一端排序后得到的最长上升子序列就是建桥的数量 数据范围为 1e5, 朴素过不了, 这里用优化版

代码

const int N = 2e5 + 10;
typedef pair<int, int> PII;
PII town[N];
int f[N];
 
int n;
 
int main()
{
    FasterIO;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> town[i].first >> town[i].second;
    sort(town + 1, town + n + 1);
 
    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
 
        int l = 0, r = cnt;
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (f[mid] < town[i].second)
                l = mid;
            else
                r = mid - 1;
        }
        cnt = max(cnt, r + 1);
        f[r + 1] = town[i].second;
    }
    cout << cnt << endl;
    return 0;
}

导弹防御系统

题目

为了对抗附近恶意国家的威胁，RR 国更新了他们的导弹防御系统。

一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。

例如，一套系统先后拦截了高度为 33 和高度为 44 的两发导弹，那么接下来该系统就只能拦截高度大于 44 的导弹。

给定即将袭来的一系列导弹的高度，请你求出至少需要多少套防御系统，就可以将它们全部击落。

输入格式

输入包含多组测试用例。

对于每个测试用例，第一行包含整数 nn，表示来袭导弹数量。

第二行包含 nn 个不同的整数，表示每个导弹的高度。

当输入测试用例 n=0n=0 时，表示输入终止，且该用例无需处理。

输出格式

对于每个测试用例，输出一个占据一行的整数，表示所需的防御系统数量。

数据范围

1≤n≤50

输入样例：

5
3 5 2 4 1
0

输出样例：

2

样例解释

对于给出样例，最少需要两套防御系统。

一套击落高度为 3,4 的导弹，另一套击落高度为 5,2,1的导弹。

思路

上一题 中, 只能通过下降序列来拦截导弹, 这里这既可以用上升序列也可以用下降序列, 那么就转化为： 一个序列如何用上升序列和下降序列覆盖, 且所用序列数最小

还是从单个元素切入, 该导弹有两种覆盖情况： 情况1：被单调上升序列覆盖 情况2：被单调下降序列覆盖

似乎没有什么妙的方法, 数据量也挺小, 直接暴力搜索所有情况。

用dfs来求全局最小值有两种方法：全局变量和迭代加深。 全局变量就是声明一个res变量存最终结果, 每搜到一个结果时就与res比较, 留下最小的那个。

对于每个导弹, 先将其当做用上升子序列覆盖的题来求, 求完后再恢复。然后再用下降子序列覆盖的题来求, 求完后恢复。

求上升/下降子序列时, 用贪心优化法, 代码中没用二分的写法, 而是直接遍历出来。

代码

const int N = 55;
int q[N], up[N], down[N];
int ans, n;
 
void dfs(int u, int su, int sd)
{
    if (su + sd >= ans)
        return;
    if (u == n)
    {
        ans = su + sd;
        return;
    }
    // 当前数放入上升子序列中
    int k = 0;
    while (k < su && up[k] < q[u])
        k++;
    int t = up[k];
    up[k] = q[u];
    if (k < su)
        dfs(u + 1, su, sd);
    else
        dfs(u + 1, su + 1, sd);
    up[k] = t;
 
    // 当前数放到下降子序列中
    k = 0;
    while (k < sd && down[k] > q[u])
        k++;
    t = down[k];
    down[k] = q[u];
    if (k < sd)
        dfs(u + 1, su, sd);
    else
        dfs(u + 1, su, sd + 1);
    down[k] = t;
}
 
int main()
{
    while (cin >> n, n)
    {
        for (int i = 0; i < n; i++)
            cin >> q[i];
        ans = n;
        dfs(0, 0, 0);
        cout << ans << endl;
    }
    return 0;
}

二分法：

// 最长上升子序列, 同一位置上越小越好
	int l = -1, r = su + 1;
    while(l + 1 != r)
    {
        int mid = l + r >> 1;
        if(up[mid] < a[u]) // 求第一个>=a[u]的, 也就是r
            l = mid;
        else 
            r = mid;
    }
    int t = up[r];
    up[r] = a[u];
    if(r != su + 1) // 初始时全为0则全都是比a[u]小的, 故 r 为默认值不变
        dfs(u + 1, su, sd);
    else
        dfs(u + 1, su + 1, sd);
    up[r] = t;
// 最长下降子序列, 同一位置上越大越好
    l = -1, r = sd + 1;
    while(l + 1 != r)
    {
        int mid =l + r >> 1;
        if(down[mid] > a[u]) // 求第一个 <= a[u]的替换掉, 有可能是0（默认值）
            l = mid;
        else
            r = mid;
    }
    t = down[r];
    down[r] = a[u];
    if(r != sd) // 默认为0,故肯定能找到位置sd为0,如果确实在sd说明前面都能比a[u]大, 故增加长度
        dfs(u + 1, su, sd);
    else
        dfs(u + 1, su, sd + 1);
    down[r] = t;

最长公共上升子序列

题目

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。

小沐沐说，对于两个数列 AA 和 BB，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 AA 和 BB 的长度均不超过 30003000。

输入格式

第一行包含一个整数 NN，表示数列 A，BA，B 的长度。

第二行包含 NN 个整数，表示数列 AA。

第三行包含 NN 个整数，表示数列 BB。

输出格式

输出一个整数，表示最长公共上升子序列的长度。

数据范围

1≤N≤30001≤N≤3000,序列中的数字均不超过 231−1231−1。

输入样例：

4
2 2 1 3
2 1 2 3

输出样例：

2

思路

f[i][j] a数组中前i个数, 以b[j]为结尾的公共上升子序列 划分为包含a[i]和不包含a[i] 包含a[i]时, 枚举所有以b[j < i]为结尾的公共上升子序列, 也就是倒数第二个元素, 判断是否b[j] >= b[k] 若符合则转移

代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 3e3+ 10;
int a[N], b[N];
int f[N][N];
int n,m;
 
int main()
{
    cin >> n;
    for(int i = 1; i <= n;i ++) cin >> a[i];
    for(int i = 1; i <= n;i ++) cin >> b[i];
    
    /*
    for(int i = 1; i <= n;i ++)
        for(int j =1 ; j <= n; j++)
        {
            f[i][j] = f[i - 1][j];
            if(a[i] == b[j])
            {
                f[i][j] = max(f[i][j], 1);
                for(int k = 1; k < j; k++)
                    if(b[k] < b[j])
                        f[i][j] = max(f[i][j], f[i][k] + 1);
            }
        }
    */
    
    for(int i = 1; i <= n;i ++)
    {
        int maxv =1;
        for(int j =1 ; j <= n; j++)
        {
            f[i][j] = f[i - 1][j];
            if(a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            else if(a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }
        
    int res = 0; 
    for(int i = 1; i <= n;i ++) res = max(res , f[n][i]);
    cout << res << endl;
 
    
    return 0;
}