蒙德里安的梦想 POJ-2411
NxM的棋盘填充 1x2 的长方形，有多少种方案。
我们把所有横着的1x2长方形填充情况枚举，对于一种状态，其对应的竖着的长方形也是一定的，没有额外的枚举空间，所以就可以只考虑横着的长方形。
需要找到填到最后N行M列，且成立的所有方案数。
- 填到最后
- 成立
状态表示：从第1列到第i列，且第i列的格子是否被i-1的横方块占着的情况 j，j用二进制表示。
那么最后的结果就是 f[n + 1][0]，当第n+1列没有第n列横方块占着的情况之和便是结果。
状态计算：
第i列由第i-1列转移，每个j都有对应的可以转移过来的 j(i - 1)。
怎么判断是否可以转移过来呢？
当 j = 100100（这里的1代表在i-1列放过来的横块），首先不能从 j(i - 1) = 111111转移过来，因为当第一位为1时，说明在 i - 2 列时就被占位，不能占到第i列。
也就是说需要满足 i 列中为1的每一位， i-2 中必须对应为0。
即k & j == 0，k 为 j(i - 1)。
那么能从 j(i - 1) = 011011 转移过来吗？很明显这样的状态并不合法，只有一格无法被竖块填充。
故可以从 j(i - 1) = 001001转移。
怎样判断当前状态是否合法呢？需要保证每个0不是落单的0，若当前位为0，且
下一位为1，则往上统计0的个数（包括自己），直到遇到1。个数为奇数时，不成立。
可以优化一下，一遍顺序遍历一遍统计经过0的个数，若碰到1时就判断。
bool ok = true;
int cnt = 0;
for(int j = 0; j < n; j++)
{
if(i >> j & 1) // 若为1
{
if(cnt & 1) // 若0个数为奇数
{
ok = false; break;
}
else cnt = 0; // 为偶数，则清空计数，去统计下一次
}
else cnt++; // 为0
}那是不是 check(k) && check(j) 就够了？
这样并不行，因为 k 表示的 j(i - 1) 是由 i - 2列决定的状态，实际上还需要包括 第i列 j的因素，即 i - 1 列的状态 为 k | j，当符合 上述条件时肯定成立，但也有 或k 或j 不成立时合起来却成立的情况：
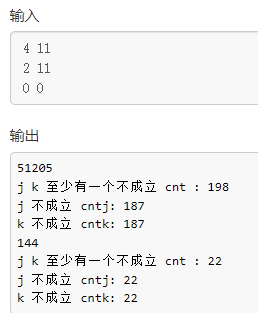则若成立，转移方程为： f[i][j] += f[i - 1][k] （k是可以转移到j的 j(i - 1)）
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 13, M = 1 << N;
typedef long long LL;
LL f[N][M];
int state[M];
vector<int> st[M];
int n,m;
bool check(int x)
{
int cnt = 0;
for(int i = 0; i < n;i ++)
{
if(x >> i & 1)
{
if(cnt & 1)
{
return false;
}
else cnt = 0;
}
else cnt++;
}
if(cnt & 1) return false;
return true;
}
int main()
{
while(cin >> n >> m, n || m)
{
memset(f, 0, sizeof f);
f[0][0] = 1;
for(int i = 1; i <= m;i ++)
{
for(int j = 0; j < 1 << n; j++)
{
for(int k = 0; k < 1 << n; k++)
{
if(((j & k) == 0)&& check(j | k))
{
f[i][j] += f[i - 1][k];
}
}
}
}
cout << f[m][0] << endl;
}
return 0;
}打表优化
上述算法时长为 1200ms，过长了，反正也需要枚举所有可能的条件，我们为何不实现把所有状态的可行性存下来然后 以O(1)查询呢
故最后得到一个二维数组 state[j]，存所有 能转移到 j 的状态。 首先是判断某个状态是否成立
bool st[M];
for(int i = 0; i < 1 << m; i++)
{
bool ok = true;
int cnt = 0;
for(int j = 0; j < n; j++)
{
if(i >> j & 1)
{
if(cnt & 1)
{
ok = false;
break;
}
else cnt = 0;
}
else cnt++;
}
st[i] = ok;
}然后求state
vector<vector<int>> state(M);
for(int i = 0; i < 1 <<m; i++)
{
state[i].clear();
if(int j = 0; j < 1 <<m; j++)
{
if((j & i) == 0 && st[i | j])
state[i].push_back(j);
}
}最后DP就行。
while(cin >> n >> m, n || m)
{
for(int i = 0; i < 1 << n; i++) st[i] = check(i);
for(int i = 0; i < 1 << n; i++)
{
state[i].clear();
for(int j = 0; j < 1 << n; j++)
{
if((j & i) == 0 && st[i | j])
state[i].push_back(j);
}
}
memset(f, 0, sizeof f);
f[0][0] = 1;
for(int i = 1; i <= m;i ++)
{
for(int j = 0; j < 1 << n; j++)
{
for(auto k : state[j])
{
if(k >= 1 << n) break;
f[i][j] += f[i - 1][k];
}
}
}
cout << f[m][0] << endl;
}积木画 LG-p8784
source: 蓝桥杯2022年第十三届省赛真题-积木画 - C语言网 (dotcpp.com) 4406. 积木画 - AcWing题库
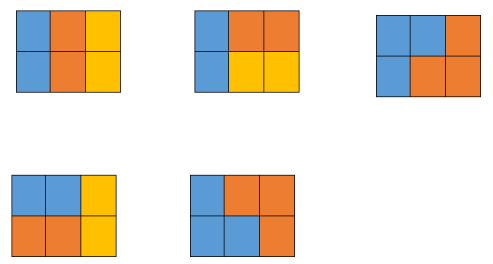n列 2行的格子，用 横方块，竖方块，楼梯方块*2 填充
与蒙德里安的梦想类似，可以用 f[i][j]表示 第i列 中的状态 j 的方案数
同样，状态为 j 时也只能从特定的状态 j(i - 1) 中转移过来
梦想题中我们是以 第 i 列，因i-1列占有的格子数为状态 j 这里就两个，所以 j 为 0 1 2，分别为 不占 ，占1个，占2个。
当 j = 0 时，说明 i - 1 列中的方块没有能伸到这一列的，推断出两种情况：
- i - 1列放一个竖块，前提是 i - 1 的状态为 0
- i - 1列啥也放不了，即 i - 1 的状态为 2
当 j = 1 时，说明 i - 1 列中的方块伸过来一个，推断出三种情况：
- i - 1列放一个横块（上面），即 i - 1的状态为 1
- i - 1列放一个横块（下面），即 i - 1的状态为 1
- i - 1列放一个朝右的楼梯块，即 i - 1的状态为 0，能放那肯定得俩都空着
当 j = 2是，说明 i - 1 列中的方块伸过来两个，推断出两种情况：
- i - 1列本身有一个格子被占，只能放一个倒过来朝左的楼梯块，即 i - 1的状态为 1
- i - 1列没格子被占，但用两横块给塞满，即 i - 1的状态为 0
于是转移方程呼之欲出 起始条件为
// 结果是 f[n + 1][0]
f[2][0] = 1; // 列数从1开始，则初始条件从 2 开始，若n为1，则会输出 f[2][0]
f[2][1] = 2; // 若能用到这个状态，则n肯定大于1，那么第1列的状态为0，下一列的可能占用状态个数就是2(两种梯子方块)
f[2][2] = 1; // 同上，不过是两个横块最终代码：
#include <iostream>
using namespace std;
const int N = 1e7 + 10;
const int MOD = 1e9 + 7;
int f[N][3];
int main()
{
int n;
cin >> n;
f[2][0] = 1;
f[2][1] = 2;
f[2][2] = 1;
for (int i = 3; i <= n + 1; i++)
{
f[i][0] = (f[i - 1][0] + f[i - 1][2]) % MOD;
f[i][1] = ((f[i - 1][0] * 2)%MOD + f[i - 1][1]) % MOD; // 因为 * 2 容易溢出所以再加个 MOD
f[i][2] = (f[i - 1][1] + f[i - 1][0]) % MOD;
}
cout << f[n + 1][0] << endl;
}最短Hamilton路径 旅行商问题
给定一张 n 个点的带权无向图，点从 0∼n−1 标号，求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输出格式
输出一个整数，表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤10^7
输入样例：
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例：
18
解题思路
这题最重要的是要不重不漏的经过每一个点且经过的路径最短。
既然是跟图有关那先考虑一下图论的算法可不可以解决： 图的深度优先搜索可以实现, 保存当前路径并且判断是否不重不漏。 但时间复杂度起码为 20!, 不能用暴力方法。
试试优化一下暴力做法, 列出一次暴力过程来看：
0 → 1 → 2 → 3 0 → 2 → 1 → 3 …
这两种情况对于后续遍历的贡献（即3之后 → 4等等）, 只在于经过了哪几个点, 经过的顺序无所谓（因为1 → 2 和 2 → 1 的权值相同） , 且点不同时只保留总权值最小的, 后续的遍历就只以最小的为基础。
假设一个状态表示：
- 经过哪几个点
- 结尾为特定点 可以代表上述点相同最小状态。
那么状态表示 f[i][j] 就可以, i 是二进制表示有几个数被选上, j 为结尾数
怎么转移呢？
假设 f[i][j] 由 f[state_k][k] 转移
state_k 需要保证 j 没有被选上, 然后加上 k → j 的权值
即 f[i][j] = f[state_k][k] + w[k][j]
怎么枚举能转移到 j 的这个 state_k 呢？
首先 j 要已经被选上, 即 i 的 第 j 位 为 1
那么 k 的状态就需要还没选上 j, 即 state_k = i - (1 << j)
接着该状态需要包含 k, 即 (state_k >> k) & 1
然后再加上权值即可
完整代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int f[M][N];
int w[N][N];
int n;
int main()
{
cin >> n;
for(int i = 0; i < n;i ++)
for(int j = 0; j < n; j ++)
{
scanf("%d", &w[i][j]);
}
memset(f, 0x3f, sizeof f);
f[1][0] = 0;
for(int i = 0; i < 1 << n; i++)
{
for(int j = 0; j < n; j++)
{
if(i >> j & 1)
{
for(int k = 0; k < n; k++)
{
if(i - (1 << j) >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
}
}
}
}
cout << f[(1 << n) - 1][n - 1] << endl;
return 0;
}踩方格
有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：
a. 每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；
b. 走过的格子立即塌陷无法再走第二次；
c. 只能向北、东、西三个方向走；
请问：如果允许在方格矩阵上走 n 步，共有多少种不同的方案。
2 种走法只要有一步不一样，即被认为是不同的方案。
输入格式
允许在方格上行走的步数 n(n≤20)。
输出格式
计算出的方案数量。
Input
2
Output
7
思路
走0步有 1 种方案, 不走。 走1步有三种方案, 左右上。 走第二步的时候就可以根据上一步来, 正常来说从三个方向的第一步来, 应该是 3 + 3 + 3 = 9 方案 但要求不能从之前走过的一步, 简单分析得： 不能从重新走往上的步, 所以不需要考虑向北走重复, 但有可能从左右走到重复位置。 故当往左走到i点时, i - 1点只能从左和上走到, 走右到 i - 1 的话就重复 当右走到i点时, i - 1 点只能从右和上走到, 走左也重复 当上走到i点时, i - 1 点可以从左和右和上走到
展开！
状态表示： f[i][j] i表示步数, j表示从那个方向走到 0左 1右 2上
状态属性： 数量
状态计算：
f[i][0] = f[i - 1][0] +f[i - 1][2];
f[i][1] = f[i - 1][1] +f[i - 1][2];
f[i][2] = f[i - 1][0] + f[i - 1][1] + f[i - 1][2];Corn Fields
农场主John新买新牧场，这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12)，每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草，供他的奶牛们享用。
遗憾的是，有些土地相当贫瘠，不能用来种草。并且，奶牛们喜欢独占一块草地的感觉，于是John不会选择两块相邻的土地，也就是说，没有哪两块草地有公共边。
John想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择？（当然，把新牧场完全荒废也是一种方案）
Input
第一行：两个整数M和N，用空格隔开。
第2到第M+1行：每行包含N个用空格隔开的整数，描述了每块土地的状态。第i+1行描述了第i行的土地，所有整数均为0或1，是1的话，表示这块土地足够肥沃，0则表示这块土地不适合种草。
Output
一个整数，即牧场分配总方案数除以100,000,000的余数。
Sample Input
2 3
1 1 1
0 1 0Sample Output
9
思路
蒙德里安那道题的一种应用, 依然是用二进制来表示该列上哪个位置种草。 总思路就是枚举所有可行状态, 然后计算转移, 最后得出结果方案数。
直接迁移思考路径, 先考虑怎样的一列是成立的： 题目要求任意两块草坪不能相邻, 相比于蒙德里安要简单一些, 只需要用个计数来判断是否存在相邻草坪即可
for(int i = 0; i < 1 << n; i++)
{
bool cnt = false, flag = false;
for(int j = 0; j < n; j++)
{
if(i >> j & 1) // 这一位是1, 种草坪
{
if(cnt) // 如果相邻一位也是1
{
flag = true;
break;
}
else cnt = true;
}
else cnt = false;
}
if(!flag) ...; // 如果成立再进行下一步操作
}接着考虑某一个状态可以从哪个状态中转移过去：
设 第i列 当前状态为 j, i - 1列 状态为 k, 初始状态可以转移
当出现相邻1时, 不能转移（不成立）：
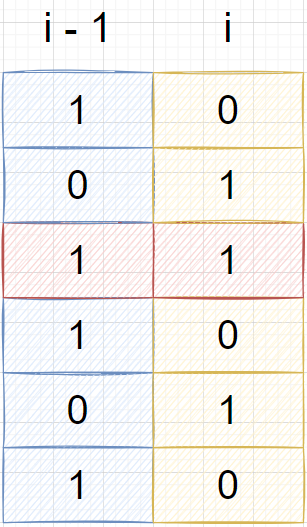
故需要满足 k & j == 0。
题目上还有一个条件, 有的地方是不能种草坪的, 所以在判断某列是否成立时, 需要加上判定：
for(int k = 1; k <= n; k++)
for(int i = 0; i < 1 << m; i++)
{
bool cnt = false, flag = false;
for(int j = 0; j < m; j++)
{
if(i >> j & 1) // 这一位是1, 种草坪
{// k 表示某一列, 这里无论j是否能将题目中数组对应上二进制的位置, 对结果没有影响, 因为需要在意的只是相对位置
if(cnt || g[k][j] == 0) // 如果相邻一位也是1
{
flag = true;
break;
}
else cnt = true;
}
else cnt = false;
}
if(!flag) ...; // 如果成立再进行下一步操作
}最后的结果怎么求： 遍历最后一列的所有状态, 将其加起来即可。
for(int i = 0; i < 1 <<m; i++)
{
if(check(i))
res += f[n][i];
}对于当前列状态是否有效还有一种更巧判断方法：
判断是否存在相邻1可以 (x&(x >> 1)) && (x&(x <<1)) 若左/右移后再&结果不为0 则说明存在相邻, 整个表达式返回0时才说明状态存在。
判断是土地是否肥沃可以先将输入处理成同样的状态表示 map[i] , 若状态 x 可以存在, 说明 x & map[i] == x。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
//------- Coding Area ---------//
const int N = 15,M = 1 << N, MOD = 100000000; // M是状态
int n, m;
int g[N][N], f[N][M], map[N];
long long res;
bool check(int k,int x) // 第k列的状态x
{
bool flag1 = (x & (x >> 1)) && (x & (x << 1));
bool flag2 = (x & map[k]) != x;
return !(flag1 || flag2);
}
int main()
{
cin >> m >> n;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
cin >> g[j][i];
// 处理输入
for (int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
map[i] = (map[i] << 1) + g[i][j];
}
// 起始状态计算
for (int i = 0; i < 1 << m; i++)
if (check(0,i)) f[0][i] = 1;
// 开始DP
for (int i = 1; i < n; i++)
{
for (int j = 0; j < 1 << m; j++)
{
for (int k = 0; k < 1 << m; k++)
{
if ((j & k) == 0 && check(i, j) && check(i - 1, k))
f[i][j] = (f[i][j] + f[i - 1][k]) % MOD;
}
}
}
// 找出答案
for (int i = 0; i < 1 << m; i++)
{
if (check(n - 1, i)) res = (res + f[n - 1][i]) % MOD;
}
cout << res << endl;
return 0;
}单词接龙
单词接龙是一个与我们经常玩的成语接龙相类似的游戏，现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”（每个单词都最多在“龙”中出现两次），在两个单词相连时，其重合部分合为一部分，例如 beast和 astonish，如果接成一条龙则变为 beastonish ，另外相邻的两部分不能存在包含关系，例如 at 和 atide 间不能相连。
输入格式
输入的第一行为一个单独的整数 n (n \le 20)n(n≤20) 表示单词数，以下 nn 行每行有一个单词，输入的最后一行为一个单个字符，表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。
输出格式
只需输出以此字母开头的最长的“龙”的长度。
样例说明
连成的“龙”为 atoucheatactactouchoose
Sample 1
Input
5
at
touch
cheat
choose
tact
aOutput
23思路
参考：题解 P1019 【单词接龙】 - FeTieTer - 洛谷博客 (luogu.com.cn)
！！该解法不是标准解法, 因为题目数据太水所以可行！！
因为每个单词都可以选两次, 但状压DP只能选一次, 所以需要将单词复制一份
复制一份之后 n *= 2, 会导致状态大小超出 int 2^32 范围 (1 << 32), 从而 MLE（内存超限）
不过该题经测试 n <= 8, 所以 状态数 为 1 << 16 就能过。
---正文---- 状态压缩就是将所有能选的情况化为二进制01来表示, 然后计算状态转移, 最后得出结果。
这里的状态就是单词选择情况。
上一题是用 第i - 1列 转移到 第i列, 这里则是从 没选择第i个单词的情况 到 选择第i个单词的情况。
状态表示： f[i][j] i是二进制表示所有单词的选择情况, j表示以第j个单词结尾
状态属性： max
状态计算： f[i][j] = max(f[i][j], f[q][k] + len[k][j]);
q表示没有选上第j个单词的状态, k表示q状态的结尾单词
len[k][j] 就是j接到k单词后面所增加的长度
最后的结果需要在计算过程中找最大值：
ans = max(ans, f[i][j]);
如何得到len数组呢： 两层循环枚举所有单词, 对于 单词a 和 单词b： 当 a b 互不包含, 且 a单词末尾存在与b单词开头相同的部分时, b可以接在a后面
判断a b是否互不包含：
string a, b;
if((strstr(a.c_str(), b.c_str())
|| strstr(b.c_str(). a.c_str()))
&& a.size() != b.size()) // a==b 时不算包含
return 不能接;判断a b是否可以接上且接上后增加多少长度：
for(int k = a.size() - 1; k >= 0; k++)
{
if(a[k] == b[0])// 当找到a中一个与b起始字母相同的便开始判断
{
int j = 0, i = k;
for(i,j; i < a.size(), j < b.size(); i++,j++)
if(a[i] != b[j]) break; // 这个选点不对
if(i == a.size() - 1) return b.size() - j; // b.size() - j 即是增加长度
}
return -1;
}加起来就是怎样判断b是否能接到a：
int check(string a, string b)
{
if((strstr(a.c_str(), b.c_str()) || strstr(b.c_str(), a.c_str()) && a.size() != b.size())) return -1;
for (int k = a.size() - 1; k >= 0; k++)
{
if (a[k] == b[0])
{
int i = k, j = 0; // 双指针算法
for (; i < a.size(), j < b.size(); i++, j++)
if (a[i] != b[j]) break;
if (i == a.size() - 1) return b.size() - j;
}
}
return -1;
}计算len：
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i == j) continue;
else {
int t = check(word[i], word[j]);
if (t == 0) t = -1; // 为了省时间把不增加的也给表示成无法接上
lens[i][j] = t;
}得到len数组之后, 就可以开始DP啦: 初始条件处理
char tmp; cin >>tmp;
for (int i = 0; i < n; i++)
{
if (word[i][0] == tmp)
{
f[1 << i][i] = word[i].size(); // 1 << i 是只选中第i个单词的状态
ans = max(f[1 << i][i], ans);
}
}代码
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
//------- Coding Area ---------//
const int N = 1010, M = 1 << 16; // M是状态
int n, m;
string word[N];
int f[M][17], lens[N][N];
int check(string a, string b)
{
if((strstr(a.c_str(), b.c_str()) || strstr(b.c_str(), a.c_str())) && a.size() != b.size()) return -1;
for (int k = a.size() - 1; k >= 0; k--)
{
if (a[k] == b[0])
{
int i = k, j = 0; // 双指针算法
for (; i < a.size() && j < b.size(); i++, j++)
if (a[i] != b[j]) break;
if (i == a.size()) return b.size() - j;
}
}
return -1;
}
int main()
{
memset(f, -1, sizeof f);
cin >> n;
for (int i = 0; i < n; i++) cin >> word[i];
for (int i = n; i < n * 2; i++) word[i] = word[i - n]; // 复制一份
n *= 2;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i == j) continue;
else {
int t = check(word[i], word[j]);
if (t == 0) t = -1;
lens[i][j] = t;
}
getchar(); // 吃换行
char tmp;
cin >> tmp;
int ans = 0;
// dp初始状态处理
for (int i = 0; i < n; i++)
{
if (word[i][0] == tmp)
{
f[1 << i][i] = word[i].size();
ans = max(f[1 << i][i], ans);
}
}
// 开始dp
for (int i = 0; i < (1 << n); i++)
{
for (int j = 0; j < n; j++) // 准备选第j个单词
{
if ((i >> j) & 1) continue; // 若已经选上则返回
for (int k = 0; k < n; k++)
{
if (((i >> k) & 1) && lens[k][j] != -1 && f[i][k] != -1)
{// 若当前状态k已被选上 且 j能接到k后面 且 转移前状态已被计算
f[i | (1 << j)][j] = max(f[i | (1 << j)][j], f[i][k] + lens[k][j]);
ans = max(ans, f[i | (1 << j)][j]);
}
}
}
}
cout << ans << endl;
return 0;
}骑士
#10170. 「一本通 5.4 例 1」国王 - 题目 - LibreOJ (loj.ac)
题目
题目描述
在nxn的棋盘上放k个国王，国王可攻击相邻的8个格子，求使它们无法互相攻击的方案总数。
输入格式
只有一行，包含两个整数n和k。
输出格式
每组数据—行为方案总数,若不能够放置则输出0。
样例 1
input
3 2output
16对于全部数据,。
思路
第二行怎么摆完全只跟上一行有关系, 只需要考虑上一层的状态就可以了。把这一行的所有摆的状态用一个集合来表示。
状态机是用时序方式来分解, 状态压缩是用二进制的方式来转化为集合。
状态表示： f[i][j][s] 所有只摆在前i行, 已经摆了j个国王, 并且第i行摆放的状态是s的所有方案的集合。
状态转移：
对于第i行的状态s, 其上一行的可行状态j需要满足以下条件：
- 内部没有相邻的棋子
- 不能和第i行相互攻击到
转化为二进制, 设第
i行状态为a, 第i - 1行状态为b： (a & b) == 0a | b不能有两个相邻的1
若状态合法, 直接加上其方案数量, 语言描述为：
f[i][j][a]：已经摆完了前i排, 并且第i排的状态为a, 已经摆了j个国王的所有方案。
f[i - 1][j - count(a)][b]：已经摆完其i-1排, 并且第i-1排的状态是b, 已经摆了 j-count(a) 个国王的所有方案。
时间复杂度：状态数量 * 状态转移的计算量, 即
, S为状态, Sh为S能转移的合法状态
最坏情况10*100*1000*1000 = 1e9
但这里不是所有状态都合法。
经暴力计算, 所有合法的状态可转移的状态乘积只有1365, 那么最后的复杂度为10*10*1365 = 1.365*1e6
最暴力的方式来算时间复杂度会发现超过了上限, 但实际上用到的合法状态并没有这么多。
小技巧：
__builtin_popcount(i): 求i的二进制中1的个数
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 12, M = 1 << 10, K = 110;
long long f[N][K][M];
int n, k;
vector<int> state;
vector<int> head[M];
int cnt[M];
bool check(int s)
{
if (((s << 1) & s) && ((s >> 1) & s))
return false;
else
return true;
}
bool check(int a, int b)
{
if ((a & b) == 0 && check(a | b))
return true;
return false;
}
int getSum(int s)
{
return __builtin_popcount(s);
}
int main()
{
cin >> n >> k;
for (int i = 0; i < 1 << n; i++)
{
if (check(i))
{
state.push_back(i);
cnt[i] = __builtin_popcount(i);
}
}
for (int i = 0; i < state.size(); i++)
{
for (int j = 0; j < state.size(); j++)
{
int a = state[i], b = state[j];
if (check(a, b))
head[a].push_back(b);
}
}
f[0][0][0] = 1;
for (int i = 1; i <= n + 1; i++)
{
for (int j = 0; j <= k; j++)
{
for (auto a : state)
{
int c = cnt[a];
for (auto b : head[a])
{
if (j >= c)
f[i][j][a] += f[i - 1][j - c][b];
}
}
}
}
cout << f[n + 1][k][0] << endl;
return 0;
}玉米田 poj 3254
农夫约翰的土地由个小方格组成，现在他要在土地里种植玉米。 非常遗憾，部分土地是不育的，无法种植。 而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。 现在给定土地的大小，请你求出共有多少种种植方法。 土地上什么都不种也算—种方法。
输入格式
第行：包含两个整数和。
第行：每行包含个整数或，用来描述整个土地的状况，表示该块土地肥沃，表示该块土地不育。
输出格式
输出总种植方法对取模后的值。
数据范围
输入样例;
2 3
1 1 1
0 1 0
输出样例:
9
思路
相比于上一题, 该题存在不育的土地, 每行的状态依赖于土地情况。且有无限个玉米种子。
状态表示： f[i][j] 只种前i行, 当前行的种植情况为j 的总方案数
状态转移：
对于第i行的状态a, 其上一行的可行状态j需要满足以下条件：
- 内部没有相邻的玉米
- 不能和第i行相邻 转化为二进制为：
(a & b) == 0check(b)
若状态成立则转移方程为：
f[i][a] += f[i - 1][b]
时间复杂度：
N*M*M = 12*4096*4096 = 2e8
因为状态并非都合法, 故可行。
#include <iostream>
#include <cstring>
#include <vector>
#include <stdlib.h>
#include <stdio.h>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n,m;
int g[N];
vector<int> state;
vector<int> head[M];
int f[N][M];
inline bool check(int s)
{
if (((s << 1) & s) && ((s >> 1) & s))
return false;
else
return true;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++)
{
int t;
cin >> t;
g[i] += !t << j;
}
}
for(int i = 0; i < 1 << m; i++)
{
if(check(i))
state.push_back(i);
}
for(int i = 0; i <state.size(); i++)
for(int j = 0; j < state.size();j ++)
{
if(!(state[i] & state[j]))
head[i].push_back(j);
}
f[0][0] = 1;
for(int i = 1; i <= n + 1; i++)
{
for(int a = 0; a < state.size(); a++)
{
for(int b : head[a])
{
if(state[a] & g[i]) continue;
f[i][a] = (f[i][a] + f[i - 1][b]) % mod;
}
}
}
cout << f[n + 1][0] << endl;
return 0;
}
炮兵阵地
题目
炮兵阵地 - LibreOJ 10173 - Virtual Judge (csgrandeur.cn)
https://vjudge.csgrandeur.cn/problem/LibreOJ-10173/origin
司令部的将军们打算在 的网格地图上部署他们的炮兵部队。一个 的地图由 行 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数，分别表示 和 ；
接下来的 行，每一行含有连续的 个字符（P 或者 H），中间没有空格。按顺序表示地图中每一行的数据。
输出格式
仅一行，包含一个整数 ，表示最多能摆放的炮兵部队的数量。
样例
input
5 4
PHPP
PPHH
PPPP
PHPP
PHHPoutput
6
思路
类似于玉米地, 不过这里的影响范围是两格的十字行。也就是说在计算第i行时, 需要考虑第i-1行和第i-2行。
于是再加一维表示i-1行的状态, 然后枚举i-2行的状态来转移。
状态表示：f[i][j][k] 只安排前i行, 其中第i行的状态为j, 第i-1行的状态为k, 所有情况的安排数量最大值。
状态计算： 设第i行状态为a, 第i-1行状态为b, 第i-2行状态为c, 他们需要满足的条件为：
- 内部无相邻间隔小于两格的
- 上下行之间不能有相同列的
- 士兵不能在山地上 转化成二进制为：
(s >> 1 & s | s >> 2 & s) | (s << 1 & s | s << 2 & s) == 0((a & b) | (a & c) | (b & c)) == 0(g[i] & a | g[i - 1] & b) == 0若成立则转移方程为：f[i][a][b] = max(f[i][a][b], f[i - 1][b][c] + count(a));
时间复杂度：
n*M*M*M = 100*1000*1000*1000 = 1e12
但因为本次条件更加严格, 故可行
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 110, M = 1 << 10;
int g[N];
int f[2][M][M]; // 滚动数组优化
vector<int> state;
vector<int> head[M];
int n, m;
inline bool check(int s)
{
if (((s >> 1 & s) || (s >> 2 & s) || (s << 1 & s) || (s << 2 & s)) == 0)
return true;
return false;
}
int count(int i)
{
return __builtin_popcount(i);
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (char c; j < m && cin >> c; ++ j)
g[i] += (c == 'H') << j;
for (int i = 0; i < 1 << m; i++)
{
if (check(i))
state.push_back(i);
}
for (int i = 0; i < state.size(); i++)
for (int j = 0; j < state.size(); j++)
{
if (!(state[i] & state[j]))
head[i].push_back(j);
}
for (int i = 1; i <= n + 2; i++)
{
for (int a = 0; a < state.size(); a++)
{
for (int b = 0; b < state.size(); b++)
{
for (int c = 0; c < state.size(); c++)
{
if (g[i] & state[a] | g[i - 1] & state[b])
continue;
if (state[a] & state[b] | state[a] & state[c] | state[b] & state[c])
continue;
f[i & 1][a][b] = max(f[i & 1][a][b], f[(i - 1) & 1][b][c] + count(state[a]));
}
}
}
}
cout << f[(n + 2) & 1][0][0] << endl;
return 0;
}方伯伯的玉米田
#2211. 「SCOI2014」方伯伯的玉米田 - 题目 - LibreOJ (loj.ac)
题目描述
方伯伯在自己的农田边散步，他突然发现田里的一排玉米非常的不美。这排玉米一共有N株，它们的高度参差不齐。
方伯伯认为单调不下降序列很美，所以他决定先把一些玉米拔高，再把破坏美感的玉米拔除掉，使得剩下的玉米的高度构成一个单调不下降序列。方伯伯可以选择一个区间，把这个区间的玉米全部拔高1单位高度，他可以进行最多K次这样的操作。拔玉米则可以随意选择一个集合的玉米拔掉。
问能最多剩多少株玉米,来构成一排美丽的玉米。
输入格式
第一行包含两个整数N，K，分别表示这排玉米的数目以及最多可进行多少次操作。 第二行包含N个整数，第i个数表示这排玉米，从左到右第i株玉米的高度。
输出格式
输出一个整数，最多剩下的玉米数。
样例
input
3 1
2 1 3output
3。