公共子序列

如果两个序列完全相同长度为n，一个的子序列数量是 2^n，暴力会超时，所以要用DP

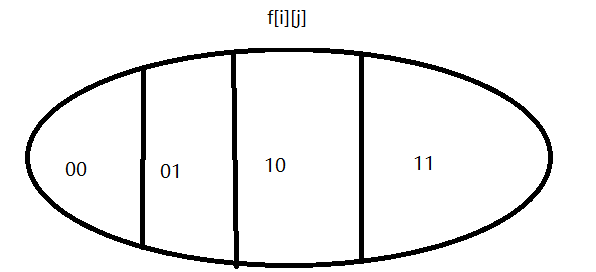状态计算如上（这种分类为不重不漏） 01 代表缺少第i个但包含第j个 00 代表俩都缺少

从11开始分析，因为要满足包含 a[i]和b[j]，所以a[i]和b[j] 一定是相等当他们相等时，这个集合中每一个公共子序列如下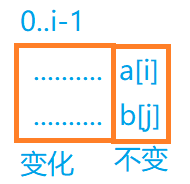：这个f[i][j]的值便是前面变化的公共子序列中的最大值加上1，也就是 f[i - 1][j - 1] + 1

至于00，则显然是 f[i - 1][j - 1]

01时不能用 f[i -1 ][j] 代表，因为此时表示的是在 (0, i -1) 和 (0, j) 中选出的最长公共子序列，但不一定选到 j，有可能会变成 f[i - 1][j - 1]的结果

原则：求数量要保证不重不漏，但求最大值的时候重复可以所以可以使用 f[i - 1]f[j]，因为包含 b[j] 的情况也在里面

由此可得，f[i - 1][j - 1]会包含在 01 10 的情况中，故我们只需要求 01 10 11 的最值即可 状态转移： f[i][j] = max(f[i - 1][j], f[i][j-1]) or max(f[i - 1][j - 1] +1) if a[i] == b[j]

优化写法：

因为只会用到 i - 1, j - 1 可以优化为 f[2][2] 只需要将上面的模板对 i % 2 即可。

for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                if (a[i] == b[j])
                    f[i % 2][j % 2] = max(f[i % 2][j % 2], f[(i - 1) % 2][(j - 1) % 2] + 1);
                else
                    f[i % 2][j % 2] = max(f[i % 2][(j - 1) % 2], f[(i - 1) % 2][j % 2]);
            }
        }
        cout << f[n % 2][m % 2] << endl;

输出最长的序列

不能用优化写法, 保存所有路径。

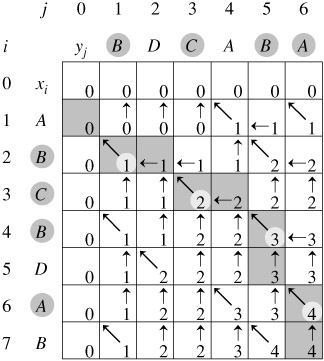
我们转移是从 上, 左, 斜左上方向转移过来, 逆序思考：斜左上转移时即说明 a[i] == b[j] 且该点选中, 加入结果中。左和上转移时判断上左哪个和当前相等, 然后转移。

最后得到的就是逆序结果, 再逆序输出即可

int i = n, j = m;
while (i >= 1 && j >= 1)
{
	if (a[i] == b[j])
		s += b[j], i--, j--;
	else if (f[i - 1](#) > f[i](#))
		i--;
	else
		j--;
}
reverse(all(s));
cout << s << endl;

合并单词(公共子序列)

title: 题目
合并 apple 和 peach 的最短长度, 结果为 appleach。
若有多个结果输出任意一个, 如 cranberry 和 boysenberry 可以输出 boysecranberry 或者 craboysenberry。
 
单词长度不超过100, 请使用优化做法。
输入包含多组数据, 以EOF为结尾。

title: input
apple peach
ananas banana
pear peach

title: output
appleach
bananas
pearch

title: 思路
 
很显然的思路是找到两个单词最长公共子序列, 删去其在另一个单词的位置,然后拼接。
找到并保存最长公共子序列的内容参考[[#输出最长的序列|这个]]
拼接似乎很麻烦, 不过可以直接在找最长序列的同时存下：
之前存内容时只存了 `a[i] == b[j]`, 这里可以把 向左, 向上 转移的字符也存下。
注意最后可能没到 `a[0],b[0]` 需要加上剩余的字符。

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>
#include <set>
using namespace std;
const int N = 1e3 + 10;
int f[N][N];
 
int main()
{
 
    string a, b;
    while (cin >> a >> b)
    {
 
        mem(f, 0);
        a = "1" + a, b = "2" + b;
        int n = a.size() - 1, m = b.size() - 1;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                if (a[i] == b[j])
                    f[i][j] = max(f[i][j], f[(i - 1)][(j - 1)] + 1);
                else
                    f[i][j] = max(f[i][(j - 1)], f[(i - 1)][j]);
            }
        }
        // 找最长公共子序列
        string s;
        int i = n, j = m;
        while (i >= 1 && j >= 1)
        {
            if (a[i] == b[j])
                s += b[j], i--, j--;
            else if (f[i - 1][j] > f[i][j - 1])
                s += a[i--];
            else
                s += b[j--];
        }
        while (i)
            s += a[i--];
        while (j)
            s += b[j--];
        reverse(all(s));
        cout << s << endl;
        string s;
    
    }
 
    return 0;
}

最短编辑距离

动态规划就是对爆搜的优化嘛

状态表示f[i][j] 表示将 a[1 ~ i] 变成 b[1 ~ j] 的操作数，值为 min 比如 f[2][4] 就表示让 a[1~~2] 代表的串变为 b[1~~4]的操作数，很明显会有增加操作

状态计算：考虑状态转移的时候，从最后一步操作入手，先考虑没发生这个操作时，集合的状态是什么，然后是进行这一步操作后产生的下一个集合状态。本题来说，分为三个操作：

删除操作：把a[i]删掉后 a[i - 1] 与 b[j] 匹配，那么操作之前的状态为 f[i - 1][j]，转移过来的话就是加一个操作步骤 f[i - 1][j] + 1
插入操作：把a[i] 插入一个数后与 b[j] 匹配，说明之前的状态是 a[i] 匹配 b[j - 1] ，因为插入的是 b[j] 这个数，所以原状态为 f[i][j - 1] 转移过来的话就是个f[i][j - 1] + 1;
替换操作：把 a[i] 改成 b[j] 之后匹配，说明操作之前 a[1 ~ (i - 1)] 与 b[1 ~ (j - 1)]匹配，则原状态为 f[i - 1][j - 1]，转移过来的话就是 f[i - 1][j - 1] +1;
若本来a[i] == b[j] 我们就不需要操作，直接用上一个的状态 f[i - 1][j - 1] + 0;

初始化操作：因为状态表示f[i][j]是a[i] 匹配 b[j] 的操作数则 f[0][j] 时的操作数就是 j ，一直添加同理 f[i][0] 也是一直删减

编辑距离2：给定n个字符串，再给定m个询问，计算每个询问中的询问串str变成 s[n] 所用操作数小于 limit 的个数

如何获得第一个字符为空的数组的长度，如 cin >> s + 1：strlen(s + 1); 用 a[N][12] 存给定的n个字符串对于m个询问，每一次询问都要分别对n个字符串计算一次最短编辑距离，所以就可以写一个edit_distance函数来封装这个操作

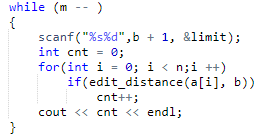
函数内的内容

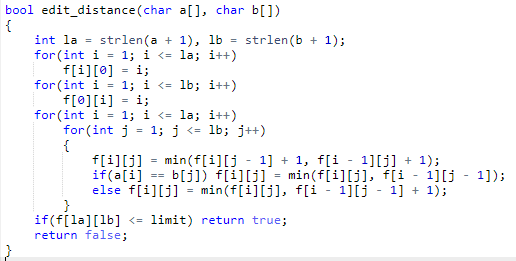
最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入样例：

7
3 1 2 1 8 5 6

输出样例：

解题策略

直观解法

N < 1000 时可以被划分为一个个子问题：当前数是否可以加到之前的序列的尾部

从中间找一个数 i, 可以加入的序列是以 0-i 之间数为结尾的序列当结尾的数小于 i 时, 则可以加入取所有结果的最大值

状态表示：f[i] 0-i之间的以i结尾的最长上升子序列
状态属性：max
状态转移：f[i] = max(f[i], f[0-i] + 1)
	当 a[0-i] 的数小于 a[i] 时

核心代码：

for(int i = 0; i < n;i ++) 
{
	f[i] = 1;
	for(int j = 0; j < i; j++)
	{
		if(a[j] < a[i])
			f[i] = max(f[i], f[j] + 1);
	}
}
 
for(int i = 0; i < n;i ++)
	ans = max(ans, f[i]);
cout << ans << endl;

N很大时

上述算法中, 由于第二层循环会尝试所有可能, 找到最大的放到 f[i] 中, 导致时间复杂度很高

是否可以找到一个方法把这层循环优化优化呢？子问题依然是当前数是否可以加到之前的序列的尾部但所加入的序列中, 有一个最优序列, 结尾数值小且长度长的序列是最好的。也就说只要能快速根据一个数找到它最应该去的序列就行

如何实现？需要一种数据组织方式来实现这两个条件：数值小, 长度长不能再沿用之前的f[i], 有很多冗余信息两个变量求极值, 得先固定一个求另一个的一元极值, 然后把所有的再求一次最大值。例如求结尾数值为3的最长长度, 结尾数值为4的最长长度

如何查找当前数的最优加入序列呢？找所有以比这个数小的数为结尾的序列长度最大值也就是从-10^9遍历到当前数

这肯定从时间上就不行,而且这其中有相当多用不上的位置

那就从长度入手求长度为2的最小结尾数, 长度为3的最小结尾数

长度从是从0开始的正整数, 上限为原数组长度

咋求呢？从大到小遍历长度, 第一个小于该数的便是最大长度然后将长度+1, 设定该长度的最小结尾数为该数

最终答案就是最长的有数的长度

需要找到一种数据结构满足以下条件：存在 key→value 的映射 key可以被理解为长度, 数据范围为0-原数组长度 value可以被理解为数字, 数据范围为 -10^9 — 10

显然map就可以满足, 但还有个最优解—数组下标为key, 值为value

所以！开展！

新的状态表示为： f[i] 长度为 i, 结尾数值为 f[i] 
状态属性：min(数值)
状态转移：存在 f[i - 1] < a[j] 时 f[i] = a[j]

怎么找到 f[i - 1] 呢？二分呗

cnt = 0; // 记录当前最长的长度
for(int i = 0; i < n;i ++)
{
	int l = 0; r = cnt; // r = cnt因为没必要从最最后面开始搜
	while(l < r)
	{
		int mid = (l + r + 1) >> 1;
		if(a[i] > f[mid]) l = mid;
		esle r = mid - 1;
	}
	cnt = max(cnt, r + 1); // 是否更新cnt
	f[r + 1] = a[i];
}
cout << cnt << endl;

如果找不到呢？ f[r + 1] = a[i] 就会把长度为1的序列更新为 a[i] 这咋保证f[i]上的数一定是最小的呢？肯定是当前最小, 后面有更小的会直接替换掉

开餐馆

蒜头君想开家餐馆. 现在共有 n 个地点可供选择。蒜头君打算从中选择合适的位置开设一些餐馆。这 n 个地点排列在同一条直线上。我们用一个整数序列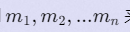来表示他们的相对位置。由于地段关系, 开餐馆的利润会有所不同。我们用 pi 表示在 mi 处开餐馆的利润。

为了避免自己的餐馆的内部竞争,餐馆之间的距离必须大于 k。

请你帮助蒜头君选择一个总利润最大的方案。

输入

输出

40
30

解题策略

为什么能用DP解题？其子问题是第 i 个餐馆是否开, 当前餐馆开了之后的利润加上 0-i 之间餐馆开的利润就是总利润

状态表示： f[i] 第i个餐馆开了之后的利润 状态属性： max 状态计算： f[i] = max(f[i], f[j] + p[i]) f[j] 为满足 m[i] - m[k] > k 的餐馆开了之后的最大利润

核心代码：

for(int i = 0; i < n;i ++)
{
	f[i] = p[i]; // 初始值设定为：只开自己的
	for(int j = i - 1; j >= 0; j--)
	{
		if(m[i] - m[j] > k)
		{
			f[i] = max(f[i], f[j] + p[i]);
		}
	}
}
 
int ans = 0;
for(int i = 0; i < n;i ++)
	ans = max(ans, f[i]);
cout << ans << endl;

魔法少女

废墟一共有 n 层，而且每层高度不同，这造成小炎爬每层的时间也不同。不过当然，小炎会时间魔法，可以瞬间飞过一层或者两层[即不耗时]。但每次瞬移的时候她都必须要至少往上再爬一层（在这个当儿补充魔力）才能再次使用瞬移。爬每单位高度需要消耗小炎 1 秒时间。消灭魔女之夜是刻不容缓的，所以小炎想找你帮她找出一种最短时间方案能通往楼顶。

输入格式

第一行一个数字 N(1≤N≤10000)，代表楼层数量。

接下去 N 行，每行一个数字 H(1≤H≤100)，代表本层的高度。

输出格式

输出一行，一个数字 S，代表通往楼顶所需的最短时间。

Input

Output

思路

第 i 层楼可以从 i - 1 层爬上来, 也能从 i - 1, i - 2层传送上来但传送的前提是, i - 1, i - 2层时爬上去的

展开 状态表示： f[i][j] j <= 2 i表示楼层, j=0 表示传送, j = 1表示手动 状态属性： min 状态计算：

f[i][0] = min(f[i - 1][0], f[i - 1][1]) + w[i];
f[i][1] = min(f[i - 1][0], f[i - 2][0]);

代码

#include <iomanip>
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <set>
#include <cmath>
#include <unordered_map>
using namespace std;
typedef pair<int, int> PII;
//------- Coding Area ---------//
const int N = 1e4 + 10;
int w[N];
int f[N][2];
 
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    for (int i = 1; i <= n; i++)
    {
        f[i][0] = min(f[i - 1][0], f[i - 1][1]) + w[i];
        f[i][1] = min(f[i - 1][0], f[i - 2][0]);
    }
    cout << min(f[n][0], f[n][1]) << endl;
    return 0;
}

Lighting System Design

紫书9-6 你的任务是设计一个照明系统。一共有n(n≤1000)种灯泡可供选择，不同种类的灯泡必须用不同的电源，但同一种灯泡可以共用一个电源。

每种灯泡用4个数值表示：电压值 V(V≤132000), 电源费用K (K⩽1000), 每个灯泡的费用C(C≤10) 所需灯泡的数量 L(1⩽L⩽100)。

假定通过所有灯泡的电流都相同，因此电压高的灯泡功率也更大。为了省钱，可以把一些灯泡换成电压更高的另一种灯泡以节省电源的钱(但不能换成电压更低的灯泡)。

你的任务是计算出最优方案的费用。

输入样例

3
100 500 10 20
120 600 8 16
220 400 7 18
0

输出样例

思路

每一种灯泡都有固定的选择数目, 我们需要做的是找到最佳替换方案, 来使费用最低。

费用由电源费和灯费组成, 对于电源费来说, 若该灯全部替换, 则会省下电源费, 显然对于一种灯只有全部替换和不替换的选择：有两个 V = 100的, 其中一个替换走, 仍然需要付电源费, 若两个都替换, 则可以省下电源费。

s[i] 表示 1-i 的总灯泡数, 用前缀和求出。

状态表示： f[i] 1 - i 中的电费 状态属性： min 状态计算： f[i] = min(f[i], f[j] + (s[i] - s[j]) * c[i] + k[i])

代码

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1e3 + 10;
int f[N], s[N];
struct Bomb
{
    int v, k, c, l;
    bool operator<(const Bomb &W) const
    {
        return v < W.v;
    }
} a[N];
 
int main()
{
    int n;
    while (cin >> n && n)
    {
        for (int i = 1; i <= n; i++)
        {
            int v, k, c, l;
            cin >> v >> k >> c >> l;
            a[i] = {v, k, c, l};
        }
        sort(a + 1, a + 1 + n);
        mem(f, 0x3f);
        f[0] = 0;
        for (int i = 1; i <= n; i++)
        {
            int v = a[i].v, k = a[i].k, c = a[i].c, l = a[i].l;
            s[i] = s[i - 1] + l;
            for (int j = 0; j < i; j++)
            {
                f[i] = min(f[i], f[j] + (s[i] - s[j]) * c + k);
            }
        }
        cout << f[n] << endl;
    }
    return 0;
}

Partitioning by Palindromes

紫书9-7 输入一个由小写字母组成的字符串，要求把它划分成尽量少的回文串。输出最少的个数。
如aaadbccb最少可以划分为3个：aaa,d,bccb

输入：
第一行输入一个n表示数据组数
接下来n行每行输入一个字符串s(1⇐s⇐1000)

输出：
输出一个数表示最少的个数输入样例

3
aaadbccb
ffgcc
juzi

输出样例

3
3
4

思路

线性DP问题。将所有可能的回文串标记出来, 存入 s[i][j] 表示 i-j 这个串是不是回文串。

判断当前字符是否可以与之前的串构成回文串, 如果可以则当前的最短长度为该回文串的上一个 最短长度。如判断第i个字符, 可以构成以第j个字符开头, 第i个字符结尾的回文串, 则至此最短数量就是 f[j - 1] + 1, 这个1就是代表当前的回文串。

紫书上判断所有回文串的代码： 类似于记忆化搜索

int is_prilindrome(int i, int j)
{
	if(i >= j) return  1;
	if(s[i] != s[j]) return 0;
 
	if(vis[i][j] == kase) return p[i][j];
	vis[i][j] = kase;
	p[i][j] = is_prilindrome(i + 1, j - 1); // 当子串为回文且当前俩字符相等, 才是回文
	return p[i][j];
}

代码

#include <iostream>
#include <cstring>
 
using namespace std;
const int N = 1e3 +10;
int vis[N][N], f[N];
bool p[N][N];
char s[N];
 
int n, kase;
 
int is_prilindrome(int i, int j)
{
	if(i >= j) return  1;
	if(s[i] != s[j]) return 0;
 
	if(vis[i][j] == kase) return p[i][j];
	vis[i][j] = kase;
	p[i][j] = is_prilindrome(i + 1, j - 1); // 当子串为回文且当前俩字符相等, 才是回文
	return p[i][j];
}
 
int main()
{
	int T;
	cin >> T;
	for(kase  = 1; kase <= T; kase++)
	{
		cin >> s + 1;
		n = strlen(s + 1);
		f[0] = 0;
		for(int i = 1; i <= n; i++)
		{
			f[i] = i + 1;
			for(int j = 0; j < i; j++)
			{
				if(is_prilindrome(j + 1, i))
				{
					f[i] = min(f[i], f[j] + 1);
				}
			}
		}
		cout << f[n] << endl;
	}
	return 0;
}

🪴 Edwin Aze's Blog

最近文章

洛师薅羊毛教程

挖土机编程 CSP-J 2022 模拟赛 Round 2

我是学生如何白嫖GPT4

最近笔记

Hi~

202503051617 latex documentclass options

线性DP类

公共子序列

优化写法：

输出最长的序列

合并单词(公共子序列)

最短编辑距离

编辑距离2：给定n个字符串，再给定m个询问，计算每个询问中的询问串str变成 s[n] 所用操作数小于 limit 的个数

最长上升子序列

输入样例：

输出样例：

解题策略

直观解法

N很大时

开餐馆

输入

输出

解题策略

魔法少女

输入格式

输出格式

思路

代码

Lighting System Design

思路

代码

Partitioning by Palindromes

思路

代码

目录