棋盘分割

将一个 $8\times 8$ 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 $(n-1)$ 次后，连同最后剩下的矩形棋盘共有 $n$ 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

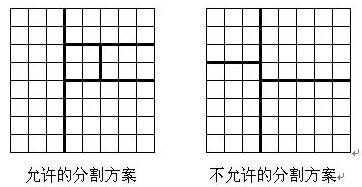
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。

现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差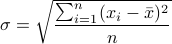 ，其中平均值 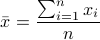，$x_i$ 为第 $i$ 块矩形棋盘的总分。

请编程对给出的棋盘及 $n$，求出均方差的最小值。

输入格式

第 1 行为一个整数 n。

第 2 行至第 9 行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式

输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围

1<n<15

输入样例：

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例：

1.633

思路

已经学了这么多分割子问题的类型, 显然这个也可以进行分割, 不过之前都是一维区间分段分割, 这里则是二维矩形分割。

状态表示： f[x1][y1][x2][y2][k] 子矩阵(x1,y1) (x2,y2)划分k个部分的最小方差均值。 状态计算： 一个矩阵划分可以竖着划分, 共 (y2 - y1 - 1) * 2种切法, 乘2是因为可以选择保留左边还是右边。 或者横着划分, 共 (x2 - x1 - 1) * 2种切法。 令v = f[x1][y1][x2][y2][k] 竖切：

• 取上v = min(f[x1][y1][i][y2][k - 1] + get(i, y1, x2, y2)) i in [x1, x2)
• 取下v = min(f[i][y1][x2][y2][k - 1] + get(x1,y1,i,y2)) i in [x1, x2) 横切：
• 取左v = min(f[x1][y1][x2][i][k - 1] + get(x1, i, x2, y2)) i in [y1, y2)
• 取右v = min(f[x1][i][x2][y2][k - 1] + get(x1, y1, x2, i)) i in [y1, y2) 这里用递归的写法会更好, 递推太繁琐了。

代码

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
#include <iomanip>
#include <cmath>
using namespace std;
 
int readInt()
{
    int t;
    cin >> t;
    return t;
}
 
#define debug
//------- Coding Area ---------//
const int N = 16, M = 10;
const double INF = 0x3f3f3f3f;
double f[M][M][M][M][N];
double X;
int a[M][M];
int n, m;
 
double get(int x1, int y1, int x2, int y2)
{
    double sum = a[x2][y2] - a[x1 - 1][y2] - a[x2][y1 - 1] + a[x1 - 1][y1 - 1] - X;
    return sum * sum / n;
}
 
double dfs(int x1, int y1, int x2, int y2, int k)
{
    double &v = f[x1][y1][x2][y2][k];
    if (v >= 0)
        return v;
    if (k == 1)
        return get(x1, y1, x2, y2);
    v = INF;
    // 竖切
    for (int i = y1; i < y2; i++)
    {
        v = min(v, dfs(x1, y1, x2, i, k - 1) + get(x1, i + 1, x2, y2));
        v = min(v, dfs(x1, i + 1, x2, y2, k - 1) + get(x1, y1, x2, i));
    }
    // 横切
    for (int i = x1; i < x2; i++)
    {
        v = min(v, dfs(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));
        v = min(v, dfs(i + 1, y1, x2, y2, k - 1) + get(x1, y1, i, y2));
    }
 
    return v;
}
 
int main()
{
    setPrec(3);
    FasterIO;
    cin >> n;
    m = 8;
    for (int i = 1; i <= 8; i++)
        for (int j = 1; j <= 8; j++)
        {
            cin >> a[i][j];
            a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
        }
    X = (double)a[m][m] / n;
    memset(f, -1, sizeof f);
 
    cout << sqrt(dfs(1, 1, 8, 8, n));
    return 0;
}