#10178. 「一本通 5.5 例 4」旅行问题 - 题目 - LibreOJ (loj.ac) John 打算驾驶一辆汽车周游一个环形公路。公路上总共有 n 车站,每站都有若干升汽油(有的站可能油量为零),每升油可以让汽车行驶一千米。John 必须从某个车站出发,一直按顺时针(或逆时针)方向走遍所有的车站,并回到起点。在一开始的时候,汽车内油量为零,John 每到一个车站就把该站所有的油都带上(起点站亦是如此),行驶过程中不能出现没有油的情况。
任务:判断以每个车站为起点能否按条件成功周游一周。
输入格式
第一行是一个整数 n,表示环形公路上的车站数;
接下来 n 行,每行两个整数,,分别表示表示第 i 号车站的存油量和第 i 号车站到下一站的距离。
输出格式
输出共 n 行,如果从第 i 号车站出发,一直按顺时针(或逆时针)方向行驶,能够成功周游一圈,则在第 i 行输出 TAK,否则输出 NIE。
样例
输入
5
3 1
1 2
5 2
0 1
5 4输出
TAK
NIE
TAK
NIE
TAK数据范围与提示
对于全部数据,。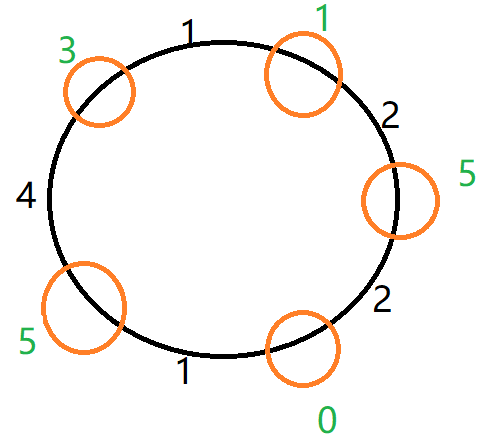
对于环形问题, 通常做法就是将其延长一倍, 然后枚举起点到长度:
for(int i = 1; i <= n; i++) s[i + n] = s[i]; // 复制一遍
for(int i = 1; i <= n; i++)
int j = i + n - 1; // 此时i-j就是循环的其中一段先考虑顺时针。 :点 点 消耗 的 油量 :到点 能 获得 的 油量
相对应的前缀和含义: :从 出发到 所 消耗 的 总油量 :从 出发到 所 获得 的 总油量
显然, 要走到 点, 需要满足 sp[i - 1] - sd[i - 1] + p[i] >= d[i], 即 走到i点时剩余油量 + i点获得油量 >= 走到 i + 1 点消耗的油量
到 的耗油: 到 的加油:
其代码形式为:
s[i] = p[i] - d[i] 当前可获得的油量减去下一步走的距离, 然后对s数组求一次前缀和, 即是走到 i + 1 位置时所剩下的油量
s[i] += s[i - 1]
for i : [1,n]
if s[i] < 0
return false显然按照这种做法, 需要再用一层循环来枚举起点, 其复杂度为, 无法通过的限制。
有一种方法可以优化终点的选取:
从起点i到终点j之间所有长度的前缀和, 其对最终答案的贡献并不相同, 因为只需要求出存在s[j] - s[i]为负数的结果即可, 那么既然s[i]已经固定, 我们找到最小的s[j]即可, 若最小的相减都不为负数, 那么其他结果也肯定为正数, 这里使用了贪心思想。
也可以用数学证明: 因为 是已经确定的, 故可视为常量提取出来:
于是问题从枚举终点变成了在长度为n的区间中找到最小值, 且这个区间会滑动, 故这里可以使用单调队列来优化。
部分代码为:
for(int i = 1; i <= n; i++) s[i] = s[i + 1] = o[i] - d[i];
for(int i = 1; i <= n; i++) s[i] += s[i - 1];
// 顺时针枚举的话得逆序
for(int i = n * 2; i ; i--)
{
if(hh <= tt && q[hh] <= i + n) hh++; // 因为是枚举起点, 故包含i
while(hh <= tt && s[q[tt]] >= s[i]) tt--;
q[++tt] = i;
if(i <= n)
res[i] = true;
}
逆时针时:
镜像分析 一下就好了,不过下标有所变化 到 的耗油: 到 的加油:
代码
const int N = 2e6 + 10;
typedef long long LL;
int n;
int o[N], d[N];
LL s[N];
int q[N];
bool st[N];
int main()
{
FasterIO;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> o[i] >> d[i];
for (int i = 1; i <= n; i++)
s[i] = s[i + n] = o[i] - d[i];
for (int i = 1; i <= n * 2; i++)
s[i] += s[i - 1];
int hh = 0, tt = -1;
for (int i = n * 2; i; i--)
{
if (hh <= tt && q[hh] >= i + n)
hh++;
while (hh <= tt && s[q[tt]] >= s[i])
tt--;
q[++tt] = i;
if (i <= n)
if (s[q[hh]] - s[i - 1] >= 0)
st[i] = true;
}
d[0] = d[n];
for (int i = 1; i <= n; i++)
s[i] = s[i + n] = o[i] - d[i - 1];
for (int i = 1; i <= n * 2; i++)
s[i] += s[i - 1];
hh = 0, tt = -1;
for (int i = 1; i <= n * 2; i++)
{
if (hh <= tt && q[hh] < i - n)
hh++;
if (i > n)
if (s[i] - s[q[hh]] >= 0)
st[i - n] = true;
while (hh <= tt && s[q[tt]] <= s[i])
tt--;
q[++tt] = i;
}
for (int i = 1; i <= n; i++)
if (st[i])
cout << "TAK\n";
else
cout << "NIE\n";
return 0;
}