理想的正方形

理想的正方形 - LibreOJ 10182 - Virtual Judge (csgrandeur.cn)

有一个 $a\times b$ 的整数组成的矩阵，现请你从中找出一个 $n\times n$ 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为三个整数，分别表示 $a,b,n$ 的值；

第二行至第 $a+1$ 行每行为 $b$ 个非负整数，表示矩阵中相应位置上的数。

输出格式

输出仅一个整数，为 $a\times b$ 矩阵中所有$n\times n$ 正方形区域中的最大整数和最小整数的差值」的最小值。

样例

Input

5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

Output

1

数据范围与提示

对于 $20\%$ 的数据 $2\le a,b\le 100,n\le 10$ 对于 $100\%$ 的数据 $2\le a,b\le 1000,n\le a,n\le b,n\le 100$，矩阵中的所有数都不超过 $10^9$。

思路

可以先求行的极值, 存到右端, 然后再以列求极值, 这样汇集到右下角的就是最终矩阵的极值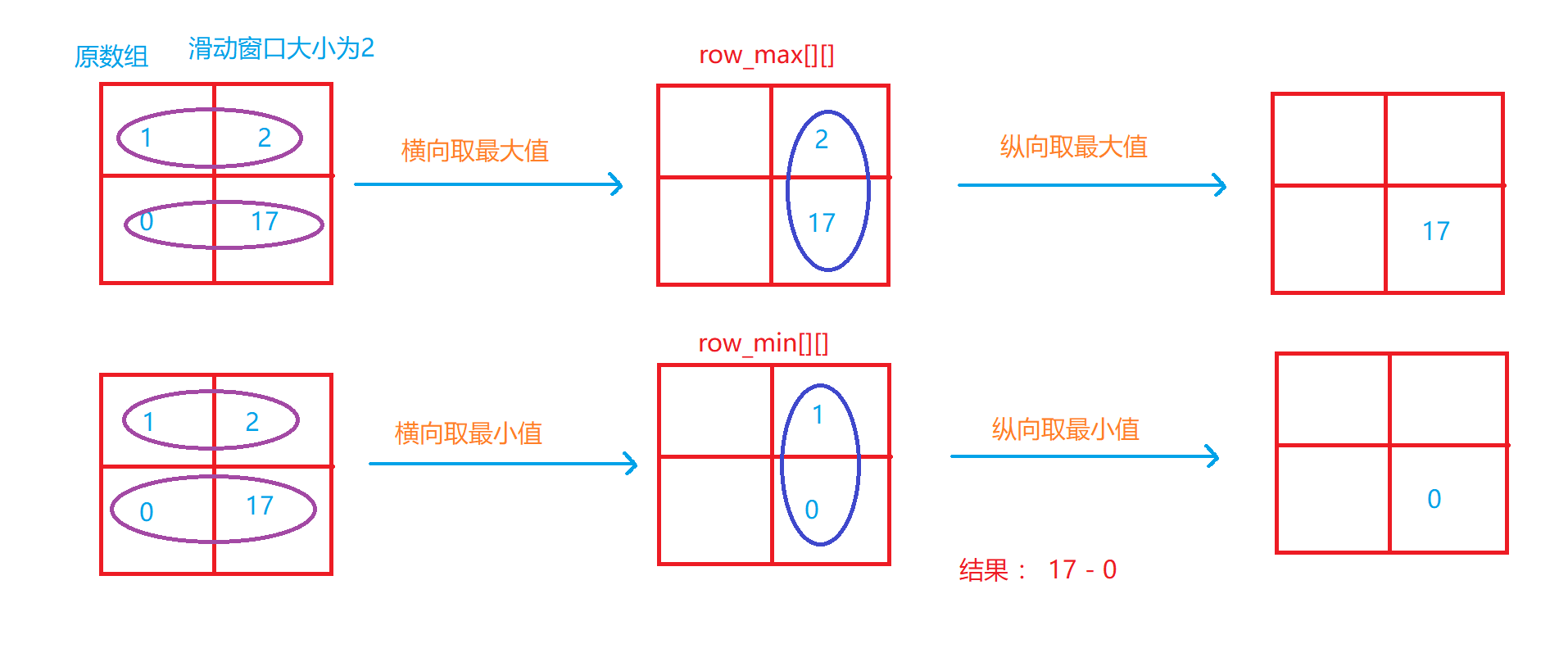时间复杂度:$O(n^2)$

代码

const int N = 1100;
int a[N][N];
int row_max[N][N], row_min[N][N];
int q[N];
int n, m, k;
 
void get_min(int a[], int b[], int tot)
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= tot; i++)
    {
        if (hh <= tt && i - q[hh] >= k)
            hh++;
        while (hh <= tt && a[q[tt]] >= a[i])
            tt--;
        q[++tt] = i;
        b[i] = a[q[hh]];
    }
}
 
void get_max(int a[], int b[], int tot)
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= tot; i++)
    {
        if (hh <= tt && i - q[hh] >= k)
            hh++;
        while (hh <= tt && a[q[tt]] <= a[i])
            tt--;
        q[++tt] = i;
        b[i] = a[q[hh]];
    }
}
 
int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
 
    // 求行
    for (int i = 1; i <= n; i++)
    {
        get_max(a[i], row_max[i], m);
        get_min(a[i], row_min[i], m);
    }
    int res = 1e9;
    int a[N], b[N], c[N];
    // 求列
    for (int i = k; i <= m; i++)
    {
        for (int j = 1; j <= n; j++)
            a[j] = row_min[j][i];
        get_min(a, b, n);
        for (int j = 1; j <= n; j++)
            a[j] = row_max[j][i];
        get_max(a, c, n);
 
        for (int j = k; j <= n; j++)
            res = min(res, c[j] - b[j]);
    }
    cout << res << endl;
    return 0;
}