股票买卖

状态机dp 把一个过程清晰的用状态机模型表示出来

股票买卖 IV

P42330. 股票买卖 IV - 题目 - LibreOJ (loj.ac) 188. 买卖股票的最佳时机 IV - 力扣（Leetcode）

给定一个长度为 $N$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 $k$ 笔交易。

注意:你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。

输入格式

第一行包含整数$N$和$k$，表示数组的长度以及你可以完成的最大交易数量。 第二行包含$N$个不超过$10000$的正整数，表示完整的数组。

输出格式

输出一个整数, 表示最大利润。

样例

input

3 2
2 4 1

output

2

思路

根据状态机模型, 分为状态：

• 当前有股票
• 当前无股票

其转移为： 买入 无股票 - w[i] ==> 有股票 卖出 有股票 + w[i] ==> 无股票

设f[i][j][2] 为第i天, 做了k个交易, 当前有无股票。则初始状态为f[i][0][0] = 0, 最终状态为max(f[n][j][0]) j 属于 0-k

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
 
int readInt()
{
    int t;
    cin >> t;
    return t;
}
 
//------- Coding Area ---------//
const int N = 1e5 + 10, M = 1e3 + 10;
int n, m, k;
int f[M][2];
int w[N];
 
int main()
{
 
    cin >> n >> k;
    for(int i = 1; i <= n; i++)
    	cin >> w[i];
    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= k; j++)
    	{
            f[j][0] = max(f[j][0], f[j][1] + w[i]);
            f[j][1] = max(f[j - 1][0] - w[i], f[j][1]);
        }
    }
    int res = -0x3f3f3f3f;
    for(int i = 0; i <= k; i++)
    	res = max(res, f[i][0]);
    cout << res << endl;
    return 0;
}

股票买卖 V

309. 最佳买卖股票时机含冷冻期 - 力扣（Leetcode）

给定一个长度为 $N$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法来计算你所能获取的最大利润，在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票)

• 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。
• 卖出股票后,你无法在第二天买入股票(即冷冻期为1天)。

输入格式

第一行包含整数$N$和$k$，表示数组的长度以及你可以完成的最大交易数量。 第二行包含$N$个不超过$10000$的正整数，表示完整的数组。

输出格式

输出一个整数, 表示最大利润。

样例

input

5
1 2 3 0 2

output

3

对应的交易状态为: 买入,卖出,冷冻期,买入,卖出，第一笔交易可得利润2-1=1，第二笔交易可得利润2-0=2，共得利润1+2 = 3。

思路

状态分为：

• 无股票
• 有股票的第一天
• 有股票的大于等于2天

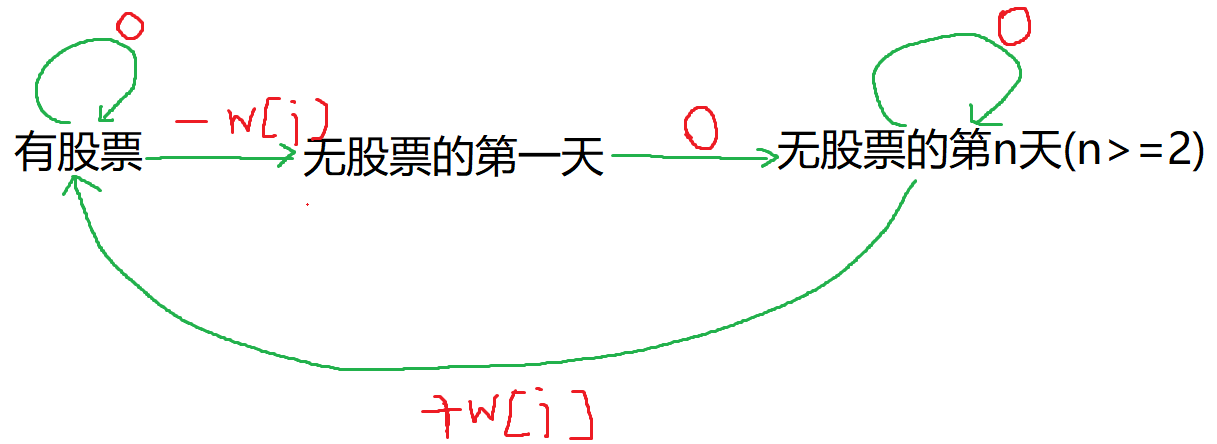
状态表示： f[i][3] 第i天, 当前有无股票 状态计算： f[i][0] = max(f[i - 1][j], f[i - 1][2] - w[i]) f[i][1] = f[i][0] + w[i] f[i][2] = max(f[i - 1][1], f[i - 1][2])

class Solution {
public:
    const int N = 5e3 + 10;
    int maxProfit(vector<int>& prices) {
        int f[N][3];
        memset(f, -0x3f, sizeof f);
        f[0][2] = 0;
        for(int i = 0; i < prices.size(); i++)
        {
            f[i][0] = max(f[i - 1 < 0?0:i-1][0], f[i - 1 < 0?0:i-1][2] - prices[i]);
            f[i][1] = f[i][0] + prices[i];
            f[i][2] = max(f[i - 1 < 0?0:i-1][1], f[i - 1 < 0?0:i-1][2]);
        }
        return max(f[prices.size()-1][1], f[prices.size()-1][2]);
    }
};