有依赖的背包问题

有 N 个物品和一个容量是 V 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

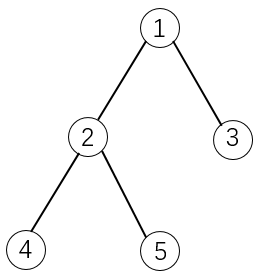
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

第一行有两个整数 N，V，用空格隔开，分别表示物品个数和背包容量。

接下来有 N 行数据，每行数据表示一个物品。 第 i 行有三个整数 vi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。 如果 pi=−1，表示根节点。 数据保证所有物品构成一棵树。

输出格式 输出一个整数，表示最大价值。

数据范围 1≤N,V≤100 1≤vi,wi≤100 父节点编号范围：

内部结点：1≤pi≤N; 根节点 pi=−1;

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

11

思路

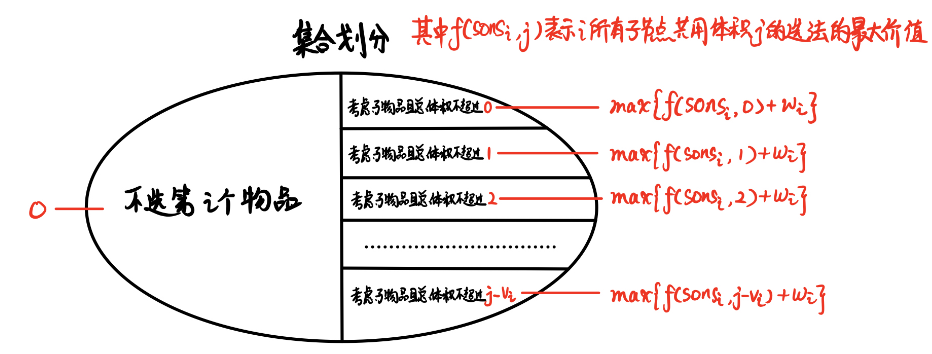
选一个物品必须选其父节点, 也就构成了树形DP。 对于根节点root, 它的子节点选法构成了一个分组背包问题。 对于每组的选法, 如果只能选一个的话就用机器分配 的单选方法, 即模板选法。 如果能选一些则可以使用 金明的预算方案的二进制状态压缩方法枚举所有。

这里则不能二进制状态压缩, 因为1 << 100 会超时, 故需采用体积划分法。 即对于每个子树, 先确定能用的最大体积, 然后再依次为基础枚举所有能用的体积来转移。

先比较一下以往 线性背包DP 的 状态转移，第 i 件 物品 只会依赖第 i−1 件 物品 的状态

如果本题我们也采用该种 状态依赖关系 的话，对于节点 i，我们需要枚举他所有子节点的组合 2k 种可能

再枚举 体积，最坏时间复杂度 可能会达到 $O(N\times 2N\times V)$（所有子节点都依赖根节点） 最终毫无疑问会 TLE

因此我们需要换一种思考方式，那就是枚举每个 状态 分给各个子节点 的 体积

这样 时间复杂度 就是 $O(N\times V\times V)$

for(int i = m - v[u]; i >= 0; i--)
	for(int j = 0; j <= i; j++)
		f[u][i] = max(f[u][i], f[u][i - j] + f[son][j]);

最后再加上root的物品。

状态表示： f[i][j] 以i为根, 背包容量为 j 的最大价值 **

代码

#include <iostream>
#include <cstring>
#include <string>
 
using namespace std;
 
const int N = 110, M = N * 2;
int h[N], e[M], v[M], w[M],ne[M], idx;
int n,m;
int f[N][N]; // 以i为根的树, 背包容量为j 时的最大价值
int root;
 
void add(int a, int b)
{
    e[idx] = b,ne[idx] = h[a], h[a] = idx++;
}
 
void dp(int u)
{
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dp(j);
        
        for(int k = m - v[u]; k >= 0; k--)
            for(int q = 0; q <= k; q++)
                f[u][k] = max(f[u][k], f[u][k - q] + f[j][q]);
    }
    for(int i = m; i >= v[u]; i--)
        f[u][i] = f[u][i - v[u]] + w[u];
    for(int i = 0; i < v[u]; i++)
        f[u][i] = 0;
}
 
int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if(p == -1) root = i;
        else {
            add(p, i);
        }
    }
    dp(root);
    cout << f[root][m] << endl;
    return 0;
}