[NOIP2018 提高组] 货币系统
题目背景
NOIP2018 提高组 D1T2
题目描述
在网友的国度中共有 种不同面额的货币,第 种货币的面额为 ,你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 、面额数组为 的货币系统记作 。
在一个完善的货币系统中,每一个非负整数的金额 都应该可以被表示出,即对每一个非负整数 ,都存在 个非负整数 满足 的和为 。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 不能被该货币系统表示出。例如在货币系统 , 中,金额 就无法被表示出来。
两个货币系统 和 是等价的,当且仅当对于任意非负整数 ,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 ,满足 与原来的货币系统 等价,且 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 。
输入格式
输入文件的第一行包含一个整数 ,表示数据的组数。
接下来按照如下格式分别给出 组数据。 每组数据的第一行包含一个正整数 。接下来一行包含 个由空格隔开的正整数 。
输出格式
输出文件共有 行,对于每组数据,输出一行一个正整数,表示所有与 等价的货币系统 中,最小的 。
样例 #1
样例输入 #1
2
4
3 19 10 6
5
11 29 13 19 17
样例输出 #1
2
5
提示
在第一组数据中,货币系统 和给出的货币系统 等价,并可以验证不存在 的等价的货币系统,因此答案为 。 在第二组数据中,可以验证不存在 的等价的货币系统,因此答案为 。
【数据范围与约定】
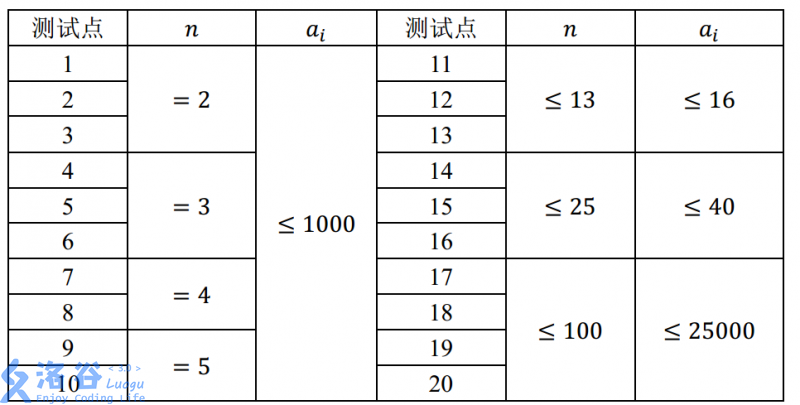
对于 的数据,满足 。
思路
题目大意:对于一个序列 , 找到他的最小序列, 满足A序列能通过 得到的所有数都能被B序列所得到, 且B序列也不能得到A序列不能得到的数。 此时两序列相等。
可以归纳出三个性质:
- 性质1: 不能被除它之外的 构成
- 性质2: B序列中的元素都源自于A序列
- 性质3: 一定能被A序列构成
性质1很显然, 满足最小条件的充分必要条件。 性质3若 不能被A构成, 但可以被B序列构成, 就无法满足序列相等条件。 性质2, 假设, 那么根据性质3, , 肯定比单独一个 大(t为正整数), 但因为 又得构建出 所以要 小于等于 , 因此, 只能从A序列中选。
至此, 我们把问题缩小到从 A 序列中选一系列数, 组成最小序列。 那么只有当前数可以被其他数所构建时, 才能消去, 正常算每个数得枚举 次, 可以通过排序(不能被比自己大的数构建)来优化一下。
从小到大枚举每个数, 并判断之前的数能不能构建出来当前的数, 可以把当前数的数值当做背包容量, 之前的数当做物品, 值当做价值, 求完全背包问题。
这里只需要求出是否恰好组成, 可以计算方案数而非最大容量。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 3e4 + 10;
int a[110];
int f[N];
int n,T;
int main()
{
cin >> T;
while(T--)
{
memset(f, 0, sizeof f);
int res = 0;
cin >> n;
for(int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + n + 1);
int m = a[n];
f[0] = 1;
for(int i = 1; i <= n; i++)
{
if(!f[a[i]]) res++;
for(int j = a[i]; j <= m; j++)
f[j] += f[j - a[i]];
}
cout << res << endl;
}
return 0;
}