整数划分
一个整数n分解为若干正整数之和，n = a + b + c + d… 求有多少种不同的分法。
暴力做法
之前做过类似的整数划分题，范围比较小，可以直接用dfs 函数为 dfs(int sum, int u) u 为枚举的位置，sum为当前总和。
完全背包做法
还有完全背包做法，看成有 n 个背包，每个物品权值为 1,2,3,4,5…n
背包容量为 n 。
完全背包问题的朴素做法为：
从结果来看，第i个物品选(0 ~ s) 个，k满足 k*i <= j
0 为 f[i - 1][j]
k 为 f[i - 1][j - k*v[i]] + k*w[i]
一层for枚举i，一层枚举j，再一层枚举k即可
对于这个问题可以直接套用
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000 + 10, MOD = 1e9 + 7;
int f[N][N];
int n;
int main()
{
cin >> n;
for(int i = 0; i <= n;i ++) f[i][0] = 1;
for(int i = 1; i <= n;i ++)
{
for(int j = 1; j <= n; j++)
for(int k = 0; k * i <= j; k++)
f[i][j] = (f[i - 1][j - k*i] + f[i][j]) % MOD;
}
cout << f[n][n] << endl;
return 0;
}注意完全背包问题 j 是从0开始，这里从1开始是因为 默认容量为0时算一种方案，而背包问题使用默认值0就可以，这个问题需要将 f[i][0] 初始化为1
优化方法也类似
f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - 2*i] + f[i - 1][j - 3*i...;
f[i][j - i] = f[i - 1][j - i] + f[i - 1][j - 2*i]...
故使用 f[i][j - i] 代替后面的，得出 f[i][j] = f[i - 1][j] + f[i][j - i]
但由于把k优化之后，k所限制的拿物品数量边界也没了，且j-i也不能为负数，所以要加个判断if(j >= i)。
代码为：
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000 + 10, MOD = 1e9 + 7;
int f[N][N];
int n;
int main()
{
cin >> n;
for(int i = 0; i <= n;i ++) f[i][0] = 1;
for(int i = 1; i <= n;i ++)
{
for(int j = 1; j <= n; j++)
if(j >= i)
f[i][j] = (f[i][j - i] + f[i - 1][j]) % MOD;
else
f[i][j] = f[i - 1][j];
}
cout << f[n][n] << endl;
return 0;
}之后还可以再进行优化为 一维，因为 f[i][j] 可以求得任何的 i, j 的方案数，而很多之前的层数只是为了推到下一层，推出来之后就不再使用，故可以只保留一维，让这次还未被刷新的，被保留的f[j] 代表上一层的f[j]，刷新过的代表这一层的 f[j]。
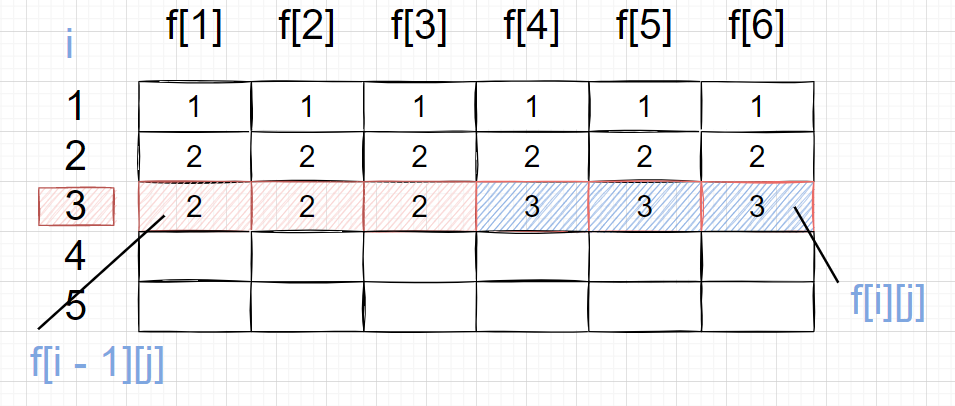但仍然是两层循环i, j，需要保证在求时每层i对应的 f[j] 是应该被用到的 f[i - 1][j]，而不是这一层提前给处理的 f[i][j]，让优化后的部分也代表原来的含义。
这也是为什么完全背包优化到一维时，j 需要从m到0枚举。
这里则可以让 j 从 小到大 从i开始枚举
f[i - 1][j] 因为 f[j] 此时正要更新，那么更新前的值就是上一层 i-1 遗留下来的值
而 f[i][j - i] 所代表的是 f[i][k] ( k ⇐ i)， 按照之前的思路if(j <= i) f[i][j] = f[i - 1][j]
是需要等于 f[i-1][k]，那么它也正是上一层未被更新的值，故可以优化为一维。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000 + 10, MOD = 1e9 + 7;
int f[N];
int n;
int main()
{
cin >> n;
f[0] = 1;
for(int i = 1; i <= n;i ++)
{
for(int j = i; j <= n; j++)
f[j] = (f[j - i] + f[j]) % MOD;
}
cout << f[n] << endl;
return 0;
}减一划分做法
根据DFS暴力的做法，还能将状态表示为 f[i][j]：总和为 i，已经有j个数的方案数
那么状态计算就需要借鉴一下之前公共子序列的思路，找到答案的一个属性，并通过删除这个属性得到一种状态，再从删除后的状态中想办法通过操作转移到当前状态。 公共子序列中是删去当前的 a[i], b[j]，状态为 f[i - 1][j - 1]。 而这个问题可以发现，可以根据最终总和是否含1来划分。（其他数理论也可行，但不如1普遍）
若含1，则将其减去得到一个之前推过的状态 f[i - 1][j - 1] （因为i,j是正序枚举） 若不含1，则将所有数都减去1，得到一个之前推过的状态 f[i - j][j]
故最后转移方程为 f[i][j] = f[i - 1][j - 1] + f[i - j][j]
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000 + 10, MOD = 1e9 + 7;
int f[N][N];
int n;
int main()
{
cin >> n;
f[0][0] = 1;
for(int i = 1; i <= n;i++)
for(int j = 1; j <= i; j++)
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % MOD;
int res = 0;
for(int i = 1; i <= n;i++) res = (res + f[n][i]) % MOD;
cout << res << endl;
return 0;
}k叉树问题
题目：知山知水，树木树人 - 计蒜客 A1211 - Virtual Judge (vjudge.net) 有一个完全k叉树，每个节点有 k 条边，权值一次为1~k。 求从起点1号开始，走到过的边权值总和为n，且有一边权 >= d的路线数。
对于线性DP问题，我们需要得到最终符合要求的结果，即 满足权值为 n，至少经过一边权值 >= d 的路线数。
类似于背包，公共子序列等等，状态的设置可以根据 最终结果所需要满足的条件来设置。
例如：
| 问题名 | 状态表示 | 最终结果条件 |
|---|---|---|
| 饭卡 HDU2546 | f[i][j] 选到第 i 个物品，且背包容量为 j 的价值最大值 | 选到第 n 个物品，背包容量为 m |
| [[线性DP类#公共子序列 | 公共子序列]] | f[i][j] 包含第一个序列的前 i 个字符，第二个序列的前 j 个字符，的公共子序列最大长度 |
| k叉树问题 | f[i][0] 表示权值总和为 i，且没遇到权值>=d的边的路线数，f[i][1] 则表示遇到 >=d | 权值总和为 n，且遇到过 >= d的权值边 |
对比可发现，k叉树问题不需要找到状态的属性，没有最大值最小值要求，求的是数量。
同公共子序列的分析思路一样，对于状态计算，我们只从结果切入考虑，对于 f[i][0] 状态，表示为当前权值为 i，且遇到过 >= d 。
那么它可以从 权值总和为 [i - k , i - 1] 的状态经过一条边转移过来，且没遇到 >= d 的边，可以表示为 f[i - k ~ i - 1][0]，则状态转移方程为 f[i][0] = f[i][0] + f[i - k ~ i - 1][0]。
为什么是从 [i - k , i - 1] 转移过来呢？因为从 f[i][0] 的上一个节点走到该节点时，权值只能为 1 ~ k，并且每个权值边都有可能被走。
对于f[i][1]，有两种可能，需要加个判断条件 if(j >= d) j 为当前权值。
对于第一种，当前权值>= d是，不论是否之前有过没有过 >= d 都符合要求，状态转移方程为 f[i][1] = f[i][1] + f[i - k ~ i - 1][1] + f[i - k ~ i - 1][0]。
对于第二种，当前权值 ⇐ d， 若之前有过则状态转移方程为 f[i][1] = f[i][1] + f[i - k ~ i - 1][0]， 若没有过则 f[i][0] = f[i][0] + f[i-k ~ i-1][0]。
故最终转移方程为
if(j >= d) f[i][1] = f[i][1] + f[i-k ~ i-1][0] + f[i-k ~ i-1][1];
else {
f[i][0] = f[i][0] + f[i-k ~ i-1][0];
f[i][1] = f[i][1] + f[i-k ~ i-1][1];
}AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, MOD = 1e9 + 7;
long long f[N][2]; // 对 1e9 + 7 取模，可能会爆int
int n, k, d;
int main()
{
while(cin >> n >> k >> d) // 注意是多组数据，虽然不知道为啥题上没说
{
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= min(i, k); j++) // 不能超出最大权值，和当前权值和
{
if (j >= d)
f[i][1] = (f[i][1] + f[i - j][1] + f[i - j][0]) % MOD;
else
{
f[i][1] = (f[i][1] + f[i - j][1]) % MOD;
f[i][0] = (f[i][0] + f[i - j][0]) % MOD;
}
}
cout << f[n][1] << endl;
}
return 0;
}
盒子与球 斯特林数
现有 r 个互不相同的盒子和 n 个互不相同的球，要将这 n 个球放入 r 个盒子中，且不允许有空盒子。问有多少种方法？
例如：有 2 个不同的盒子（分别编为 1 号和 2 号）和 3 个不同的球（分别编为 1、2、3 号），则有 6 种不同的方法：
输入格式
两个整数，n 和 r，中间用空格分隔，1≤r≤n≤10。
输出格式
一个整数，表示 n 个球放入 r 个盒子的方法数。
Input
3 2
Output
6
思路
stirling数
一个球可以新放入一个盒子, 共 j * f[i - 1][j - 1]
或者放入之前有过的盒子, j * f[i - 1][j]
状态表示： f[i][j] i为球数, j为盒子数
状态属性： 数量
状态计算： f[i][j] = j * (f[i - 1][j] + f[i - 1][j - 1])
代码
#include <iomanip>
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <set>
#include <cmath>
#include <unordered_map>
using namespace std;
typedef pair<int, int> PII;
//------- Coding Area ---------//
const int N = 23, MOD = 100003;
int f[N][N];
int n, m;
int main()
{
cin >> n >> m;
f[0][0] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= min(i, m); j++)
{
f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) * j;
}
}
cout << f[n][m] << endl;
return 0;
}