捉迷藏

二分图最大匹配 二分图最小路径点覆盖 379. 捉迷藏 - AcWing题库 Vani 和 cl2 在一片树林里捉迷藏。

这片树林里有 $N$ 座房子，$M$ 条有向道路，组成了一张有向无环图。

树林里的树非常茂密，足以遮挡视线，但是沿着道路望去，却是视野开阔。

如果从房子 $A$ 沿着路走下去能够到达 $B$，那么在 $A$ 和 $B$ 里的人是能够相互望见的。

现在 cl2 要在这 $N$ 座房子里选择 $K$ 座作为藏身点，同时 Vani 也专挑 cl2 作为藏身点的房子进去寻找，为了避免被 Vani 看见，cl2 要求这 $K$ 个藏身点的任意两个之间都没有路径相连。

为了让 Vani 更难找到自己，cl2 想知道最多能选出多少个藏身点。

输入格式

输入数据的第一行是两个整数 $N$ 和 $M$。

接下来 $M$ 行，每行两个整数 $x,y$，表示一条从 $x$ 到 $y$ 的有向道路。

输出格式

输出一个整数，表示最多能选取的藏身点个数。

数据范围

$N\le 200,M\le 30000$,
$1\le x,y\le N$。

输入样例：

7 5
1 2
3 2
2 4
4 5
4 6

输出样例：

3

思路

最小路径点覆盖 (minimum path vertex cover) 是一个有向图的问题，找出最少的路径，使得这些路径经过了所有的点。

最小路径点覆盖有两种类型：最小不相交路径覆盖 (minimum disjoint path vertex cover) 和最小可相交路径覆盖 (minimum intersecting path vertex cover)。

最小不相交路径覆盖要求每一条路径经过的顶点各不相同，而最小可相交路径覆盖允许每一条路径经过的顶点可以相同。

其中不相交的路径指的是点和边都不重复。

求解最小不相交路径覆盖数的一种方法是： 我们把每个点都拆成两个点，分为入点和出点，如果 u 到 v 有边，那么我们就让 u 的入点连向 v 的出点 ， 最后跑一下最大流或者匈牙利算法求出最大匹配。 答案就是 点的数目 - 最大匹配数。

在拆点并建边后, 图会变成这样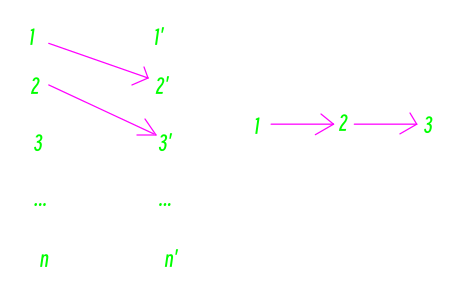： 可以发现, 拆点之后的图是一个二分图, 且每一条路径对应一个匹配, 连续匹配的终点就是一个未匹配到的点。 而最小不相交路径点覆盖的路径数量就对应左边未匹配点的数量。因为每一个未匹配点都至少需要一条路径来覆盖。

也可以用反证法。假设最小路径点覆盖数不等于顶点数减去最大匹配数，那么就会出现两种情况：

• 一种是最小路径点覆盖数小于顶点数减去最大匹配数，这意味着存在一条路径，它的尾部和另一条路径的头部相连，这两条路径就可以合并，从而减少一条路径。这与最小路径点覆盖的定义矛盾。
• 另一种是最小路径点覆盖数大于顶点数减去最大匹配数，这意味着存在一个没有被匹配的边，它连接了两个已经被匹配的顶点，那么这个边就可以和它们匹配，从而增加一个匹配对。这与最大匹配的定义矛盾。

所以，最小路径点覆盖数等于顶点数减去最大匹配数。证毕。

而求最小可相交路径点覆盖问题时, 则需要先用 Floyd 求传递闭包, 对新图中再求一次最小路径覆盖即可。

接下来证明原图的最小可相交路径点覆盖数等于新图中的最小不相交点覆盖数：

1. 对原图G进行传递闭包处理，得到新图G’，即如果在G中存在一条路径1→2→3，则在G’中添加一条边1→3。
2. 证明原图G的最小路径重复点覆盖等于新图G’的最小路径覆盖。
3. 证明≤：假设原图G有cnt条路径重复点覆盖所有点，那么对每条路径，只选择一个终点放入集合E中，这样E至多有cnt个点。由于每个点都被覆盖了，所以从E出发可以到达所有点。因此，在新图G’中，E同样是一个可行的路径覆盖方案，所以新图G’的最小路径覆盖不超过cnt。
4. 证明≥：假设新图G’有cnt个点构成了最小路径覆盖方案E，在原图G中，从这些点出发沿着原来的边走到不能走为止，得到cnt条不相交的路径。由于传递闭包保证了任意两个可达的点之间都有边相连，在原图G中也可以用这些路径覆盖所有点。因此，在原图G中，最小路径重复点覆盖不低于cnt。
5. 综上所述，原图G的最小路径重复点覆盖等于新图G’的最小路径覆盖。

该题给出一个有向无环图，有N个点M条边，选出K个点，这K个点中任意两点之间都没有路径相连。问K最大为多少。

先求出该图的最小路径重复点覆盖, 设结果为 $cnt$, 那么 $K$ 个点只能从这 $cnt$ 条路径中选择, 且为了满足任意两个 $k$ 点之间不相通, 每条路径最多选择一个点。 于是得到 $cnt\ge k$ 。接下来再构造一个结果使得 $k=cnt$ 成立, $k$ 可以取到 $cnt$, 又根据题目要求最大的 $k$ , 那么我们也就证明了 $cnt\le k$ 。

设集合$E$：$cnt$ 条路线的所有终点，总共有$cnt$个。$next(E)$ 为可以从 $E$ 中的每个点出发, 可以到达所有点的集合。 若两者交集为空集 说明从 $E$ 内任何一个点出发都无法到达其他点, 每个点都无法互相到达, 那么 $k=cnt$ 若两者交集非空 说明存在一个点 $e_i$ , 可以到达 $E$ 中其他点, 找 $e_i$ 所在的一条路径, 一定存在一个点 $e_j$ 且 $e_j$ 不属于 $next(E-e_i)$, 此时把 $e_i$ 换成 $e_j$ 即可满足互不到达且总$cnt$数不变。 $e_j$的存在性证明：如果枚举到路径起点都可以被 $next(E-e_i)$ 覆盖, 说明整条路径都可以通过其他路径到达, 和最小路径重复点覆盖的定义相悖, 可以与其他路径合并为一条路径。

故代码流程为：

1. 求传递闭包
2. 对新图拆点并求最小路径点覆盖（总点数 - 匈牙利算法最大匹配数）

【图论专题】二分图中的最小路径点覆盖问题的求解思路 - mdnice 墨滴

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
using namespace std;
const int N = 220;
bool dist[N][N];
int match[N];
bool st[N];
int n,m;
 
bool find(int u){
    
    for(int i = 1; i <= n; i++)
        if(dist[u][i] && !st[i])
        {
            st[i] = true;
            if(!match[i] || find(match[i]))
            {
                match[i] = u;
                return true;
            }
        }
    return false;
}
 
int main()
{
    cin >> n >> m;
    while(m--)
    {
        int a, b;
        cin >> a >> b;
        dist[a][b] = true;
    }
    
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                dist[i][j] |= dist[i][k] & dist[k][j];
    
    int res = 0;
    for(int i = 1; i <= n; i++)
    {
        memset(st, 0, sizeof st);
        if(find(i))
            res ++;
    }
        
    cout << n - res << endl;
    return 0;
}