许多学校与计算机网络相连。这些学校之间制定了协议：每所学校都有一份向其分发软件的学校名单（“接收学校”）。注意，如果B在学校A的分布列表中，那么A不一定出现在学校B的列表中 您需要编写一个程序，计算必须接收新软件副本的学校的最小数量，以便根据协议，软件能够到达网络中的所有学校（子任务a）。作为进一步的任务，我们希望确保通过将新软件的副本发送到任意一个学校，该软件将到达网络中的所有学校。为了实现这一目标，我们可能不得不扩大新成员的接收名单。计算必须进行的最小扩展数，以便我们将新软件发送到任何学校，它都将到达所有其他学校（子任务B）。一个扩展是指将一个新成员引入一个学校的接收名单。
第一行包含整数N：网络中的学校数（2 ⇐ N ⇐ 100）。学校由前N个正整数标识。接下来的N行中的每一行都描述了接收机列表。行i+1包含学校i的接收者的标识符。每个列表以0结尾。空列表在行中仅包含一个0。
你的程序应该向标准输出写两行。第一行应该包含一个正整数：子任务A的解。第二行应该包含子任务B的解。
input
5
2 4 3 0
4 5 0
0
0
1 0output
1
2思路
上一题做完能体会到tarjan算法的一般使用方法, 很多情况下都是tarjan接拓扑排序的思想, 关心出点和入点, 这一题也不例外。
题意是有一个有向边图, 第一个是求有多少点, 可以从该点出发到达所有点。 第二个是求需要连几条边, 使得该图为强连通图。
暴力做法遍历所有点第一个会超时, 第二个也没思路做, 这里直接考虑转化为 DAG（有向无环图）。
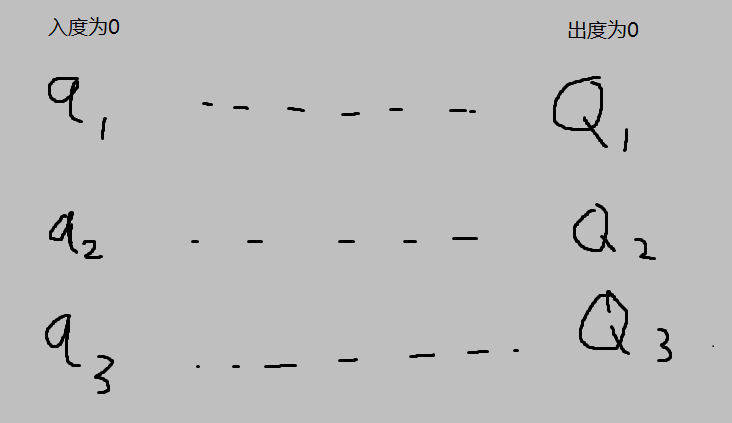q为起点, Q为终点, 对于每个起点, 没有其他点能够到达q, 所以要想从某一点到达所有点, 就必须从q起点出发, 故很显然第一个问题就是起点（入度为0的点）数量。
对于第二个问题, 假设 能够到达 , 能够到达 。（只有两个起点和两个终点, 也可以还能够到达 ） 只需要将 和 链接, 就剩下一条 和 , 再首尾连一条即可, 这种链接方法把 2个起点2个终点 转化为 1个起点1个终点, 然后再 转化为 0个起点0个终点的强连通图。
显然, 类似于动态规划问题, 可以写一个转移方程： 代表起点/终点添加边的数量, 使得整个图为强连通图。 即 那么当起点先减到0时, 剩下需要添加的边数为 当终点先减到0时, 剩下需要添加的边数为 也就说, 最终答案就是 即起点数量和终点数量的最大值。
故问题1就是起点的数量, 问题2就是起点数量和终点数量的最大值。
代码
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int stk[N], top;
bool in_stk[N];
int dfn[N], low[N], timestamp;
int n, m;
int id[N], scc_cnt;
int din[N], dout[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++timestamp;
stk[++top] = u, in_stk[u] = true;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if (in_stk[j])
low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u])
{
++scc_cnt;
int y;
do
{
y = stk[top--];
in_stk[y] = false;
id[y] = scc_cnt;
} while (y != u);
}
}
int main()
{
FasterIO;
cin >> n;
mem(h, -1);
for (int i = 1; i <= n; i++)
{
int t;
while (cin >> t && t)
add(i, t);
}
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i);
for (int i = 1; i <= n; i++)
{
for (int j = h[i]; ~j; j = ne[j])
{
int k = e[j];
int a = id[i], b = id[k];
if (a != b)
{
din[b]++;
dout[a]++;
}
}
}
int a = 0, b = 0;
for (int i = 1; i <= scc_cnt; i++)
{
if (!din[i])
a++;
if (!dout[i])
b++;
}
cout << a << "\n";
if (scc_cnt == 1)
cout << 0 << endl;
else
cout << max(a, b) << endl;
return 0;
}