最大半连通子图

tarjan强连通分量 dp 最长链数量 T4

题目描述

一个有向图 $G=\left(V,E\right)$ 称为半连通的 (Semi-Connected)，如果满足：$\forall u,v\in V$，满足 $u\to v$ 或 $v\to u$，即对于图中任意两点 $u,v$，存在一条 $u$ 到 $v$ 的有向路径或者从 $v$ 到 $u$ 的有向路径。

若 $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$ 满足 $V^{\prime }\subseteq V$，$E^{\prime }$ 是 $E$ 中所有跟 $V^{\prime }$ 有关的边，则称 $G^{\prime }$ 是 $G$ 的一个导出子图。若 $G^{\prime }$ 是 $G$ 的导出子图，且 $G^{\prime }$ 半连通，则称 $G^{\prime }$ 为 $G$ 的半连通子图。若 $G^{\prime }$ 是 $G$ 所有半连通子图中包含节点数最多的，则称 $G^{\prime }$ 是 $G$ 的最大半连通子图。

给定一个有向图 $G$，请求出 $G$ 的最大半连通子图拥有的节点数 $K$，以及不同的最大半连通子图的数目 $C$。由于 $C$ 可能比较大，仅要求输出 $C$ 对 $X$ 的余数。

输入格式

第一行包含两个整数 $N,M,X$。$N,M$分别表示图 $G$ 的点数与边数，$X$ 的意义如上文所述。

接下来 $M$ 行，每行两个正整数 $a,b$，表示一条有向边 $\left(a,b\right)$。图中的每个点将编号为 $1,2,3\dots N$，保证输入中同一个$\left(a,b\right)$不会出现两次。

输出格式

应包含两行，第一行包含一个整数 $K$，第二行包含整数 $C\mathrm{mod}X$。

样例 #1

样例输入 #1

6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4

样例输出 #1

3
3

提示

对于 $100\%$ 的数据，$N\le 10^5$，$M\le 10^6$，$X\le 10^8$。

思路

显然, 强连通分量一定是半连通的, 我们可以先把强连通分量缩点, 转化为DAG图, 然后再考虑。

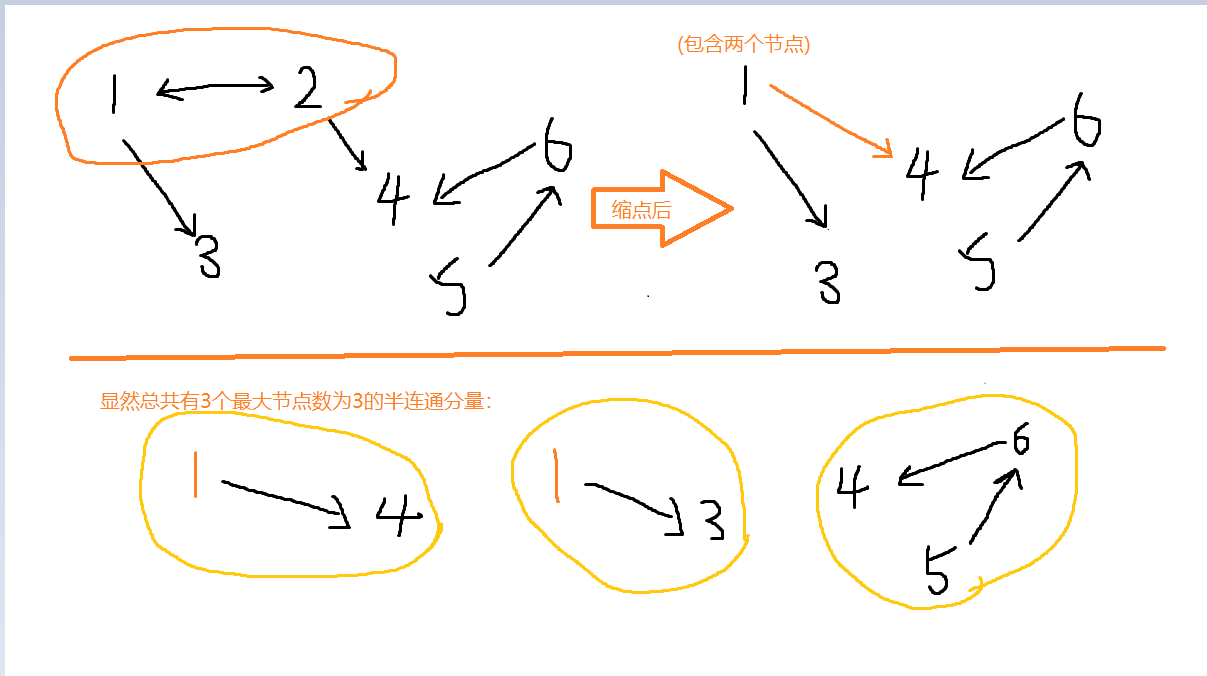如图, 很显然半连通分量就是一条直链, 不能有分叉, 因为分叉后的点没法到达另一个分叉的点（所有的双向边都缩为了一点）。

故只需要找到点数最多的链, 且求出有多少个这样的链就行。

拓扑图有个好处就是可以递推地用动态规划处理： 状态表示： f[i]: 以该点为结尾的链中节点数量 g[i]: 当前节点数量的链有几条 状态属性： f[i]: max g[i]: 数量 状态计算： 当 f[j] < f[i] + size[j] 时 f[j] = f[i] + size[j] g[j] = g[i] 更新一下数量 否则当f[j] == f[i] + size[j]时, 说明是遇到了另一条相同点数的链, 这样就加一下数量 g[j] = g[i] + g[j]

最后再遍历一遍f[i], 求出 maxf 最大点数量的半连通子图, 和 数量sum。

代码

const int N = 1e5 + 10, M = 2e6 + 10;
int n, m, mod;
// tarjan
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], size[N], scc_cnt;
 
// 最大连通图点数量, 最大连通图数量
int f[N], g[N]; 
 
// 存图
int h[N], hs[N], e[M], ne[M], idx;
 
void add(int h[], int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
 
void tarjan(int u)
{
    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u, in_stk[u] = true;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        }
        else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }
    if (low[u] == dfn[u])
    {
        ++scc_cnt;
        int y;
        do
        {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
            size[scc_cnt]++;
        } while (y != u);
    }
}
 
int main()
{
    FasterIO;
    mem(h, -1);
    mem(hs, -1);
    cin >> n >> m >> mod;
    while (m--)
    {
        int a, b;
        cin >> a >> b;
        add(h, a, b);
    }
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);
 
    unordered_set<LL> S;
    for (int i = 1; i <= n; i++)
        for (int j = h[i]; ~j; j = ne[j])
        {
            int k = e[j];
            int a = id[i], b = id[k];
            LL hash = a * 100000ll + b; // hash来去掉重边, 这里a <= 1e5, 乘上1e5然后再加上b 就不会冲突
            if (a != b && !S.count(hash))
            {
                add(hs, a, b);// 缩点建图
                S.insert(hash);
            }
        }
 
    for (int i = scc_cnt; i >= 1; i--)
    {
        if (!f[i])
        {
            f[i] = size[i];
            g[i] = 1;
        }
        for (int j = hs[i]; ~j; j = ne[j])
        {
            int k = e[j];
            if (f[k] < f[i] + size[k])
            {
                f[k] = size[k] + f[i];
                g[k] = g[i];
            }
            else if (f[k] == f[i] + size[k])
                g[k] = (g[k] + g[i]) % mod;
        }
    }
 
    int maxf = 0, sum = 0;
    for (int i = 1; i <= scc_cnt; i++)
    {
        if (f[i] > maxf)
        {
            maxf = f[i];
            sum = g[i];
        }
        else if (f[i] == maxf)
            sum = (sum + g[i]) % mod;
    }
    cout << maxf << "\n"
         << sum << "\n";
    return 0;
}