- 桥的定义
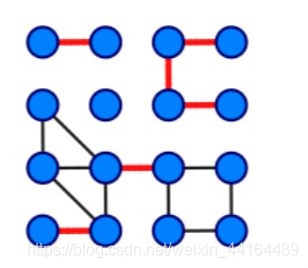
在图论中,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。
对于无向图 G 关节点(articulation vertex)/割顶(cut vertex): 如果删除某个点 后, 连通分量数目增加, 称 为图的关节点或割顶。
DFS森林的树根是否为割顶?若有两个或更多的子节点则是。 在无向连通图 的 树中, 非根节点 是 的割顶当且仅当 存在一个子节点 , 使得 及其所有后代都没有反向边连回 的祖先(连到 不算)。 就是
桥: 若 的后代只能连回 自己(即 ), 只需删除 这条边就可以让图 非连通, 这个就是桥。
Caocao’s Bridges
https://vjudge.csgrandeur.cn/problem/HDU-4738 在赤壁之战中,曹操被诸葛亮和周瑜击败。但他不会放弃。曹操的军队仍然不善于水战,所以他提出了另一个想法。他在长江建造了许多岛屿,在这些岛屿的基础上,曹操的军队很容易攻击周瑜的部队。曹操还建造了连接岛屿的桥梁。如果所有岛屿都通过桥梁相连,那么曹操的军队可以在这些岛屿中非常方便地部署。周瑜无法忍受,所以他想要摧毁一些曹操的桥梁,这样一个或多个岛屿就会与其他岛屿分开。但周瑜只有一枚由诸葛亮留下的炸弹,所以他只能摧毁一座桥。周瑜必须派人携带炸弹来摧毁这座桥。桥上可能有守卫。轰炸队的士兵数量不能低于桥梁的守卫数量,否则任务就会失败。请弄清楚周瑜至少需要多少士兵。
测试用例不超过12个。 在每个测试用例中: 第一行包含两个整数N和M,意味着有N个岛和M个桥。所有岛都从1到N编号。(2 ⇐ N ⇐ 1000,0 <M ⇐ N²) 接下来的M行描述了M个桥。每条线包含三个整数U,V和W,意味着有一个连接岛U和岛V的桥,并且在该桥上有W守卫。(U≠V且0 ⇐ W ⇐ 10,000) 输入以N = 0且M = 0结束。
对于每个测试用例,输出周瑜完成任务所需的最少士兵数量。如果周瑜无法成功,请输出-1。
输入
3 3
1 2 7
2 3 4
3 1 4
3 2
1 2 7
2 3 4
0 0输出
-1
4思路
(假设你已经做过3道以上的tarjan有向图的题, 不然还是先去做之前的训练吧, 或者查阅算法入门经典训练指南的P312页)
该图为无向图, 对于样例1来说, 是一个环, 此时无论摧毁哪条边都还是连通, 样例2则只是连通而非环, 此时可以找到最小的边摧毁。
就像之前有向边的tarjan一样, 把相互连通成环的缩小成一个点, 此时剩下的边就是摧毁后能断开的“桥”。
有向边的tarjan中需要用栈来保存当前路径, 因为只是到之前访问过的点并不一定能构成连通(有来无回)。 这里因为是无向边, 则只要是连通到之前的点就一定连通, 且这个之前的点不能是父节点。
在无向连通图 的 树中, 非根节点 是 的割顶当且仅当 存在一个子节点 , 使得 及其所有后代都没有反向边连回 的祖先(连到 不算)。 就是
桥: 若 的后代只能连回 自己(即 ), 只需删除 这条边就可以让图 非连通, 这个就是桥。
所以就在tarjan中加一条:
if(!dfn[j])
{
tarjan(j, i ^ 1); // 第二个参数传入反向边的idx
low[u] = min(low[u], low[j]);
if(low[j] > dfn[u])
res = min(res, w[i]); // w[i] 为该边的权值
}
else if(i != fa) // 若当前idx不是反向边就更新
low[u] = min(low[u], dfn[j]);这里 i = idx
如果 idx 为奇数, 则反向边为 idx - 1 = idx^1
如果 idx 为偶数, 则反向边为 idx - 1 = idx ^ 1
我们并不需要求出强连通分量的根节点之类的东西, 故仅仅以上就够。
最后需要判断该图是否连通, 如果不连通(进行了超过一次tarjan)就输出0, 因为不需要炸桥。
如果最后 res == 0 则需要输出 1, 因为至少需要一个炮兵拿炸弹。
代码
//------------------------------//
// Made by Aze //
//------------------------------//
/*
* problem:https://vjudge.csgrandeur.cn/problem/HDU-4738
* date:8/20 4:35PM
*
*/
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e3 + 10, M = 2e6 + 10, INF = 0x3f3f3f3f;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
bool bridge[M];
int dfn[N], low[N], timestamp;
int res;
void init()
{
memset(h, -1, sizeof h);
memset(e, 0, sizeof e);
memset(ne, 0, sizeof ne);
memset(dfn, 0, sizeof dfn);
memset(low, 0, sizeof 0);
memset(w, 0, sizeof w);
timestamp = idx = 0;
res = INF;
}
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void tarjan(int u, int fa)
{
dfn[u] = low[u] = ++timestamp;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfn[j])
{
tarjan(j, i ^ 1);
low[u] = min(low[u], low[j]);
if (low[j] > dfn[u]) // 如果当前j最多只能连回到j自己, 说明u->j就是一个桥
res = min(res, w[i]);
}
else if (i != fa) // 避免反向边
low[u] = min(low[u], dfn[j]);
}
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
while (cin >> n >> m && n + m)
{
init();
int cnt = 0; // 是否连通
while (m--)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
for (int i = 1; i <= n; i++)
if (!dfn[i])
{
tarjan(i, -1);
cnt++;
}
if (cnt > 1) // 不连通就不用拆
cout << 0 << endl;
else if (res == 0x3f3f3f3f)
cout << -1 << endl;
else if (res == 0)
cout << 1 << endl;
else
cout << res << endl;
}
return 0;
}