一次生日Party可能有p人或者q人参加,现准备有一个大蛋糕.问最少要将蛋糕切成多少块(每块大小不一定相等),才能使p人或者q人出席的任何一种情况,都能平均将蛋糕分食.
输入格式 每行有两个数p和q.
输出 输出最少要将蛋糕切成多少块.
对于一个有向图,
连通分量:对于分量中任意两点u, v, 必然存在从u走到v, 且从v走到u
强连通分量SCC:分量中任意两点都可以互相到达, 且加入任何一个外点之后都不是一个连通分量
一般用来把一个有向图, 通过将所有连通分量缩成一个点, 来转化为有向无环图(DAG拓扑图)

判断一个点是否在强连通分量中:
- 可以通过一个后向边到达正在祖先节点
- 走到横叉边, 然后横插边能走到祖先节点
时间戳:根据深度优先的顺序进行标号
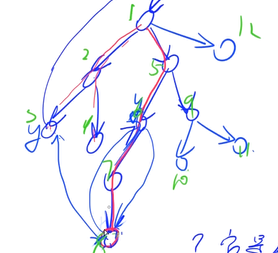
显然有以下特性: 树枝边和前向边 x < y 后向边和横叉边 x > y
定义两个时间戳:
dfs[u]: 表示遍历到u的时间戳
low[u]: 从u开始走, 能遍历到的最小时间戳
求强连通分量时求得是最高点(最靠近根的点)
就说明 dfs[u] == low[u]
栈中存的所有点都不是所在强连通分量的最高点
int dfs[N], low[N];
int stk[N], top, timestamp;
bool in_stk[N];
int scc_cnt, id[N];
void tarjan(int u)
{
dfs[u] = low[u] = ++timestamp;
stk[++top] = u, in_stk[u] = true;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfs[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if (in_stk[j])
low[u] = min(low[u], dfs[j]);
}
if (dfs[u] == low[u])
{
int y;
++scc_cnt;
do
{
y = stk[top--];
in_stk[y] = false;
id[y] = scc_cnt;
}
}
}缩点:
遍历所有点, 对于一个点能到的所有点中:
如果 j 不在同一个强连通分量, 就连一条 id[i]->id[j] 的边(i的强连通分量根节点和j的强连通分量根节点, 类似并查集的路径压缩)
缩完点后编号递减的顺序一定是拓扑顺序