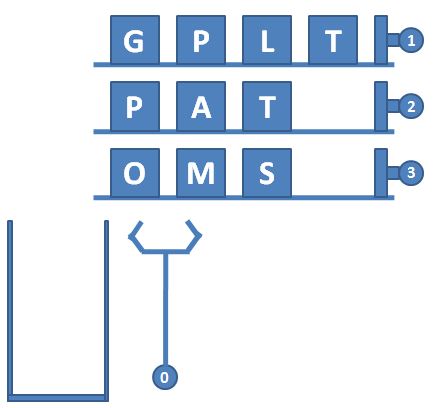
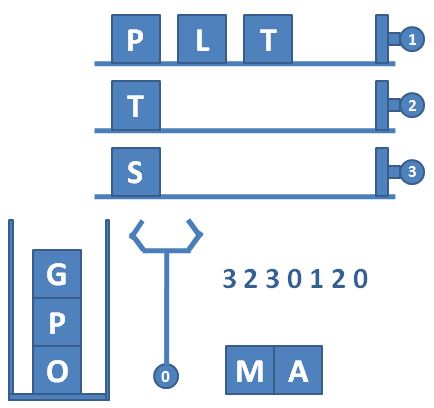
模拟 栈 T2 一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道,放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时,活塞向左推动,将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时,机械手将抓取筐顶部的一件物品,放到流水线上。图 2 显示了顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态。
图1 自动包装机的结构
图 2 顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态
一种特殊情况是,因为筐的容量是有限的,当筐已经满了,但仍然有某条轨道的按钮被按下时,系统应强制启动 0 号键,先从筐里抓出一件物品,再将对应轨道的物品推落。此外,如果轨道已经空了,再按对应的按钮不会发生任何事;同样的,如果筐是空的,按 0 号按钮也不会发生任何事。
现给定一系列按钮操作,请你依次列出流水线上的物品。
输入格式:
输入第一行给出 个正整数 N()、M()和 Smax(),分别为轨道的条数(于是轨道从 到 编号)、每条轨道初始放置的物品数量、以及筐的最大容量。随后 行,每行给出 个英文大写字母,表示每条轨道的初始物品摆放。
最后一行给出一系列数字,顺序对应被按下的按钮编号,直到 标志输入结束,这个数字不要处理。数字间以空格分隔。题目保证至少会取出一件物品放在流水线上。
输出格式:
在一行中顺序输出流水线上的物品,不得有任何空格。
输入样例:
3 4 4
GPLT
PATA
OMSA
3 2 3 0 1 2 0 2 2 0 -1输出样例:
MATA思路
N个传送带, 一个盒子, 执行多个操作, 输出最后的结果。很明显的队列与栈的模拟题。
注意是有N个传送带栈, 且是先入先出, 可以读入后用reverse反转一下。题目中的“空了就不会发生任何事”直接如果无法执行就不执行。不需要额外判断。
定义 s[110][N] 为 N 个传送带, idx[110] 为每个传送带的指针。模拟一下就行。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
using namespace std;
const int N = 1e3 + 10;
char stack[N], top;
char s[110][N];
int idx[110];
int n, m, k;
int main()
{
cin >> n >> m >> k;
for (int i = 0; i < n; i++)
{
cin >> s[i] + 1;
reverse(s[i] + 1, s[i] + 1 + m);
idx[i] = m;
}
int t;
while (cin >> t && t != -1)
{
if (t == 0 && top)
cout << stack[top--];
else
{
if(idx[t - 1])
{
if(top == k)
cout << stack[top--];
stack[++top] = s[t - 1][idx[t - 1]--];
}
}
}
return 0;
}