202503021828 数论 扩展欧几里得算法

扩展欧几里得算法

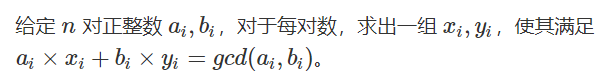
欧几里得算法为求 gcd(a, b)

该式子基于裴蜀定理。

gcd(a,b) = gcd(b, a % b) a % b = a - [a/b] * b 即: a*x + b*y = b*x + (a - [a/b]*b) * y 再进一步转化, gcd(b, a % b) = gcd(a % b, b % a % b) 且 gcd 有边界条件, 故可以通过递归来求得 x, y 当 b = 0 时, x = 1, y = 0 可得 `ax + by = ay + b(x - [a/b]*y)

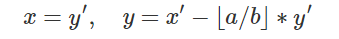
void exgcd(int a, int b, int &x, int &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return;
    }
 
    exgcd(b, a % b, x, y);
    
    int t = x;
    x = y, y = t - a/b*y;
}

线性同余方程

a*x - a*x / m * m = b 设 y = -[a*x/m] 则化为： a*x + m*y = b 显然就是 扩展欧几里得算法。 若b是 gcd(a,m) 的公约数倍数, 那就有解 那么就直接求出 exgcd(a,m,x,y)后的x, 和 gcd(a,m) , 若 b 是 gcd(a,m) 的倍数就输出 x * (b/d) % m

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
 
int exgcd(int a, int b, int &x, int &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    int t = exgcd(b, a % b, y, x);
    y = y - a/b * x;
    return t;
}
 
 
int n;
 
int main()
{
    cin >> n;
    while(n--)
    {
        int a,m,b,x,y;
        scanf("%d%d%d", &a, &b, &m);
        int d = exgcd(a,m,x,y);
        if(b % d) cout << "impossible\n";
        else printf("%d\n", (LL)x * (b / d) % m);
    }
    return 0;
}