202503021818 博弈论 SG函数

集合 SG 函数

给定  $n$  堆石子以及一个由  $k$  个不同正整数构成的数字集合  $S$。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合  $S$，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

思路

前置知识： Mex 运算： 设 S 表示一个非负整数集合.定义$mex(S)$为求出不属于集合$S$的最小非负整数运算,即: $mes(S)=minx$; 例如:$S=0,1,2,4$,那么$mes(S)=3$; SG 函数： 在有向图游戏中,对于每个节点$x$,设从$x$出发共有$k$条有向边,分别到达节点$y1,y2,\cdot \cdot \cdot \cdot yk$,定义$SG(x)$的后记节点$y1,y2,\cdot \cdot \cdot \cdot$ $yk$的$SG$函数值构成的集合在执行$mex$运算的结果,即: $SG(x)=mex(SG(y1),SG(y2)\cdot \cdot \cdot \cdot SG(yk))$ 特别地,整个有向图游戏$G$的$SG$函数值被定义为有向图游戏起点$s$的$SG$函数值,即 $SG(G)=SG(s)$. 有向图游戏的和 设$G_1，G_2,\cdot \cdot \cdot \cdot ,G_m$是$m$个有向图游戏.定义有向图游戏$G$,他的行动规则是任选某个有向图游戏$G_i$,并在$G_i$上行动一步.$G$被称为有向图游戏$G_1,G_2,\cdot \cdot \cdot \cdot \cdot ,G_m$的和. 有向图游戏的和的$SG$函数值等于它包含的各个子游戏$SG$函数的异或和,即: $SG(G)=SG(G_1)\wedge SG(G_2)\wedge \cdot \cdot \cdot \wedge SG(G_m)$

假设取石子的集合 $2,5$ , 仅有一堆石子, 石子数为 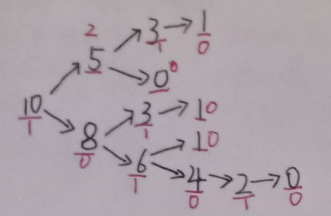$10$: 求出整个图的 SG 函数值（红色即是该节点的 SG 值） 可以发现：当 SG 值为 0 时, 从该点先手一定会输。

再根据有向图游戏的和性质, 若所有堆石子数异或后的结果为 0, 则先手必输。

计算所有 SG 函数时使用记忆化搜索, 也算枚举了所有选择的可能, 相当暴力的做法, 复杂度为指数级别。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;
const int N = 1e2 + 10, M = 1e5;
int s[N], f[M];
int k,n;
 
int sg(int x)
{
    if(f[x] != -1) return f[x];
    unordered_set<int> S;
    for(int i = 0; i < k; i++)
        if(x >= s[i]) S.insert(sg(x - s[i]));
    for(int i = 0;; i++)
        if(!S.count(i))
            return f[x] = i;
 
}
 
 
int main()
{
    memset(f, -1, sizeof f);
    cin >> k;
    for(int i = 0; i < k; i++) cin >> s[i];
    cin >> n;
    int res = 0;
    for(int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if(res) cout << "Yes\n";
    else cout << "No\n";
    return 0;
 
}