欧拉函数

公式法

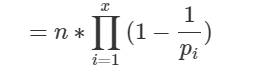
代码

int get_eurl(int n)
{
	res = n;
	for(int i = 2; i <= n / i;i ++)
	{
		if(n % i == 0)
		{
			res *= (i - 1) / i;
			while(n % i == 0)
				n /= i;
		}
	}
	if(n > 1) res *= (n - 1) / n;
	return res;
 

筛法O(n)

求多个欧拉函数时用

欧拉函数只跟该数的质因子有关, 故可以通过质数线性筛来顺便求出欧拉函数phi[N]。

for(int i = 2; i <= n;i ++)
{
	if(!st[i]) primes[cnt++] = i;
	for(int j = 0; primes[j] <= n / i; j++)
	{
		st[primes[j] * i] = true;
		if(i % primes[j] == 0) break;
	}
}

根据欧拉函数与质因子的次数无关, 当 primes[j] 本身就是 i 的一个最小质因子时, phi[primes[j] * i] = phi[i] * primes[j] 根据 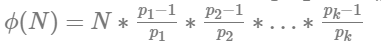后面的质因子乘积是与 phi[i] 相同, 但底数 N 不同, 故需要 乘上 primes[j]

当 primes[j] 不是 i 的质因子时, 在上式基础上还要再乘上 primes[j] 的分解式 (primes[j] - 1) / primes[j] 结果为 phi[i] * (primes[j] - 1)

LL get_eurl(int n)
{
	phi[1] = 1;
	for(int i = 2; i <= n;i ++)
	{
		if(!st[i])
		{ 
			primes[cnt++] = i;
			phi[i] = i - 1;
		}
		for(int j = 0; primes[j] <= n / i; j++)
		{
			st[primes[j] * i] = true;
			if(i % primes[j] == 0)
			{
				phi[primes[j] * i] = phi[i] * primes[j];
				break;
			}
			phi[primes[j] * i] = phi[i] * (primes[j] - 1);
		}
	}
	LL res = 0;
	for(int i = 1; i <= n ;i ++) res += phi[i];
	return res;
}