约数

小知识点

1到n中第约数个数： $\sum _{i=1}^{n}f(i)$
类似质数筛， 根据一个数是哪些数的约数来求。 $O(N\log N)$ 区间内最大约数个数的数： $0\le N\le 2\times 10^9$ , 是 $1600$ 个

试除法(sqrt(n))

从小到大判断, 如果当前数 能 整除n 就是 n的约数。 根据约数性质, 我们可以只枚举小的约数 只枚举到 n / i, 且 当 i!=n/i 时, 再把n/i（对应的大约数）放入结果

vector<int> get_divisions(int x)
{
    vector<int> res;
    for(int i = 1; i <= x / i; i++)
    {
        if(x % i == 0)
        {
            res.push_back(i);
            if(i != x/i)
                res.push_back(x/i);
        }
    }
    sort(res.begin(), res.end());
    return res;
}

约数个数

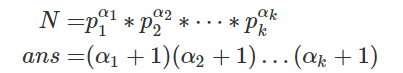每一项的βi如果不同，那么约数d就不相同（算数基本定理，每个数的因式分解是唯一的）

所以n的约数就跟βi的选法是: 对应的β1一共有0∼α1种选法 β2一共有0∼α2种选法 … βk一共有0∼αk种选法

乘法原理，一共有ans个约数

int 范围内约数个数最多的数有 1500 个左右

首先求出所有数乘积后得出来的数的分解质因数 不必全乘, 会超int, 直接算每个的, 后面算出的同样质因数就将指数加起来就行

int main()
{
    cin >> n;
    unordered_map<int,int> m;
    while (n -- ){
        int x;
        cin >> x;
        for(int i = 2; i <= x / i; i++)
            while(x % i == 0)
            {
                x/= i;
                m[i]++;
            }
        if(x > 1) m[x]++;
    }
    long long res = 1;
    for(auto i : m)
    {
        res = res * (i.second + 1) % MOD;
    }
    cout << res << endl;
    return 0;
}

约数之和

1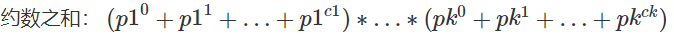

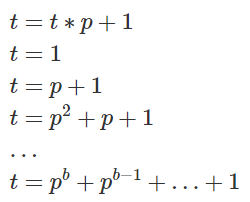
故为：

for(auto i : m)
{
	int p = i.first, a = i.second;
	long long t = 1;
	while(a--) t = (t * p + 1) % MOD;
	res = res * t % MOD;
}
cout << res << endl;

最大公约数

欧几里得算法, 辗转相除法

数论基本性质：若 d 能整除 a, 且 d 能整除 b, 那么 d 就能整除 a + b, 或 a*x + b*y

故 a 和 b 的最大公约数就可以等于 b, a % b的最大公约数

int gcd(int a,int  b)
{
	return b ? gcd(b, a % b): a;
}