组合数 逆元 加法原理 T3 #10232. 「一本通 6.6 练习 3」车的放置 - 题目 - LibreOJ (loj.ac)
题目描述
有下面这样的一个网格棋盘， 表示了对应边长度，也就是对应格子数。
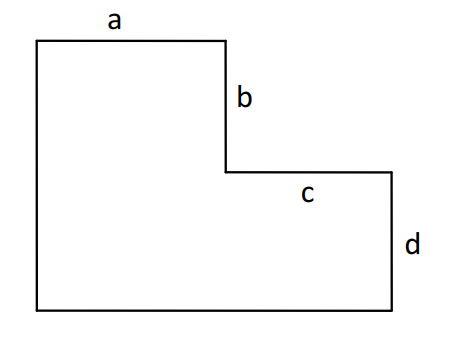
当 时，对应下面这样一个棋盘：
要在这个棋盘上放 个相互不攻击的车，也就是这 个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。同样只需要输出答案 后的结果。
输入格式
第一行为有五个非负整数 和 。
输出格式
包括一个正整数，为答案 后的结果。
样例
输入
2 2 2 2 2
输出
38
数据范围与提示
对于全部数据，，且保证了至少有一种可行方案。
思路
先上手做一个, 看有没有规律：
选择一个点（橙色点）后, 另一个能选的蓝色部分有 种。
先考虑能不能直接求得结果, 比如全排列1行4列, 为 , 为乘法原理。不能的话再分类讨论, 最后把所有情况累加起来, 用到的是加法原理。
而这道题的矩形不一定是完整的, 若是这样的一个矩形：
放 个时, 就能直接用乘法原理, 因为两个不能放在一行, 故先选行有 种方案, 确定行之后再确定放哪一列, 第一个车有 列可以选, 而第二个车就只有 个位置可以选。
故可以得到一个式子 。若 的完整矩形, 那么就是 。
因此可以启发式地思考, 看看能不能把一个不规则的图形划分为几个规则图形, 如：
上半部分选 个, 那么下半部分就选 个。
我们不可能整体上用刚才的思路, 可以采用特定的, 能不重不漏的顺序枚举所有可能, 通常是先确定一部分, 再在已经确定的部分的影响下去考虑剩下的情况, 类似于条件概率 。
这里的话上半部分方案数为： 下半部分为： 等价于
综合一下就是
当 时存在无解情况, 不过默认初始化也是 0, 不需要进行特殊处理。
该题 , 任意一种组合数算法都可以, 递推 , 而这里的 MOD 是个质数, 故也可以求出阶乘及其逆元来求解 。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 10, MOD = 1e5 + 3;
typedef long long LL;
int fact[N], infact[N];
int a,b,c,d,k;
int C(int a, int b)
{
if(a < b) return 0;
return (LL) fact[a] * infact[b] % MOD * infact[a - b] % MOD;
}
int P(int a, int b)
{
if(a < b) return 0;
return (LL)fact[a] * infact[a - b] % MOD;
}
int qmi(int a, int b, int p)
{
int res = 1;
while(b)
{
if(b & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
b >>= 1;
}
return res;
}
int main() {
fact[0] = infact[0] = 1;
for(int i = 1; i < N; i++)
{
fact[i] = (LL) fact[i - 1] * i % MOD;
infact[i] = (LL) infact[i - 1] * qmi(i, MOD - 2, MOD) % MOD;
}
cin >> a >> b >> c >> d >> k;
LL res = 0;
for(int i = 0; i <= k; i++)
res = (res + (LL)C(b,i) * P(a,i) % MOD * C(d,k-i) % MOD * P(a+c-i,k-i) % MOD) % MOD;
cout << res << endl;
return 0;
}