二进制枚举 DFS T3
ZZULIOJ
光棍节即将来临,小辣参加了某资本家的某游戏
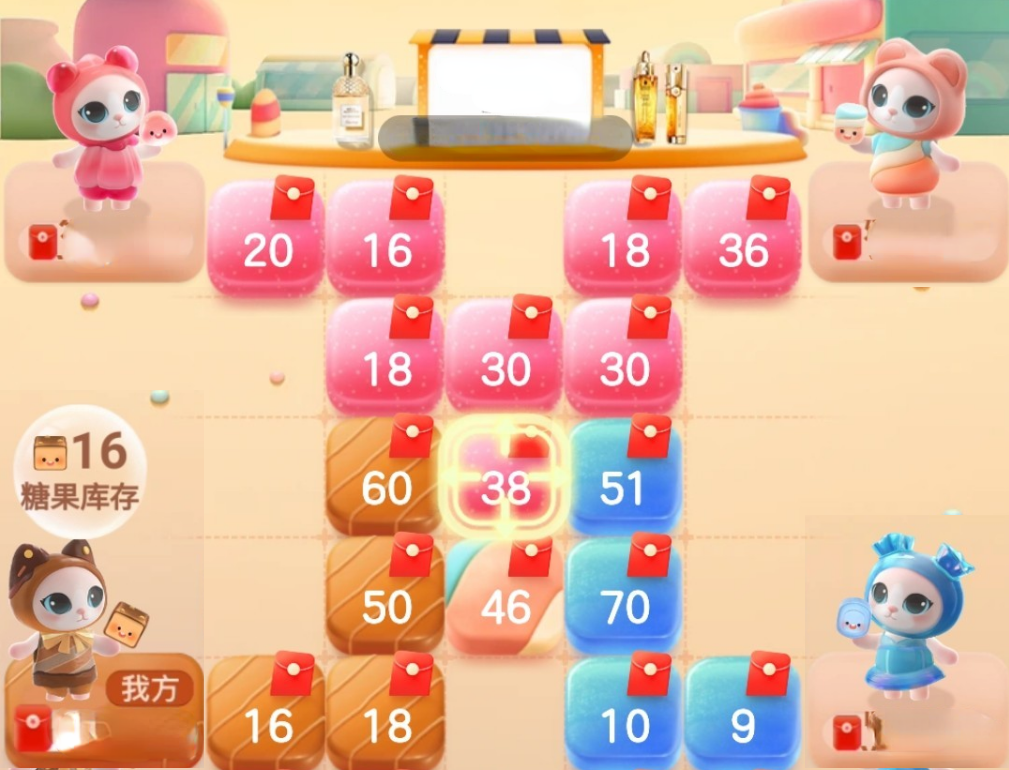
即四根光棍在如图场景进行游戏,每个格子有一个数值
你可以掷若干次骰子,每次随机掷出 1 ~ 6 之间的整数值,加入糖果库存
如果某次掷骰子后你的糖果库存大于某个格子的数值,且这个格子与你占领的格子相邻,那么你可以选择占领这个格子,占领后库存清 0
我们称两个格子相邻当且仅当有一条边重合
默认一开始你位于左下方(即图中显示“我方”的位置),也就是说只有左下方的格子与你相邻
小辣用二十年单身换取了 n 次掷骰子的机会,你能告诉他最好情况下最多能占领几个格子吗
输入
第一行一个整数 , 表示数据组数。对于每组数据:
第一行 个正整数,依次表示图中从左到右从上到下个格子的数值,前四个表示第一行四个格子,第五到七表示第二行三个,以此类推。
第二行 个非负整数 ,表示掷骰子的次数
, 保证所有数据
输出
对于每组样例输出一行一个整数,表示最多能占领的格子数量
样例输入
2
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
100样例输出
10
17思路
刚开始的思路是直接用DFS搜索, 但有的点是需要被多次经过, 比如走到1之后得回来继续走到36时, 就不能简单地使用 st 数组标记来优化步骤。
最好的方法是用二进制枚举所有点走过的方案, 然后用DFS判断当前状态是否成立。
我们设一个长度为 17 的二进制串来记录 1~17编号的格子 是否走过。对于每一个状态 , 先判断起点是否被选中, 即 是否为1。如果选中才会从该点开始搜索。
对于不规则形状的二维坐标, 且每个点都有唯一的编号, 我们可以用一个二维数组g映射 , 同时用 来实现 的映射。
DFS中, 定义一个二进制状态 来更新当前已经走过的位置, 如果当前 , 并且用的筛子数小于筛子总数, 那说明当前的状态成立。
枚举时判断 当前位置的id值 所对应的点是否被走过, 以及是否在目标状态中, 否则就返回不走。
为了方便处理, 我们把每个点的价格转化为需要用的筛子数 。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
using namespace std;
const int N = 18, M = 5;
int x[] = {1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5};
int y[] = {1, 2, 4, 5, 2, 3, 4, 2, 3, 4, 2, 3, 4, 1, 2, 4, 5};
int g[N][N];
int w[N];
int n;
int dx[] = {1, -1, 0, 0}, dy[] = {0, 0, 1, -1};
int end_state, cnt, ans;
bool dfs(int a, int b, int state)
{
if (end_state == state && cnt <= n)
return true; // 可以满足
int id = g[a][b]; // 找对应的价格
if (id == -1 || !(state >> id & 1) || (end_state >> id & 1))
return false;
end_state |= 1 << id;
cnt += w[id];
for (int i = 0; i < 4; i++)
if (dfs(a + dx[i], b + dy[i], state))
return true;
return false;
}
int main()
{
memset(g, -1, sizeof g);
for (int i = 0; i < 17; i++)
g[x[i]][y[i]] = i;
int T;
cin >> T;
while (T--)
{
ans = 0;
for (int i = 0; i < 17; i++)
cin >> w[i], w[i] = (w[i] + 5) / 6;
cin >> n;
for (int i = 0; i < 1 << 17; i++)
{
if (!(i >> 13 & 1))
continue;
end_state = 0, cnt = 0;
if (dfs(x[13], y[13], i))
ans = max(ans, (int)__builtin_popcount(i));
}
cout << ans << endl;
}
return 0;
}