每做一次决策就可以得到解的一部分,当所有决策做完之后,完整的解就“浮出水面”了。在回溯法中,每次决策对应于给一个结点产生新的子树,而解的生成过程对应一棵解答树,结点的层数就是“下一个待填充位置”cur。
9.3.1 多段图的最短路
多段图是一种特殊的DAG,其结点可以划分成若干个阶段,每个阶段只由上一个阶段所 决定。
例题9-4 单向TSP(Unidirectional TSP, UVa 116)
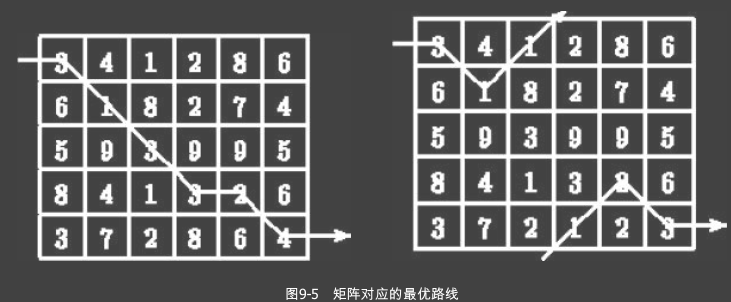
给一个m行n列(m≤10,n≤100)的整数矩阵,从第一列任何一个位置出发每次往右、右
上或右下走一格,最终到达最后一列。要求经过的整数之和最小。整个矩阵是环形的,即第
一行的上一行是最后一行,最后一行的下一行是第一行。输出路径上每列的行号。多解时输
出字典序最小的。图9-5中是两个矩阵和对应的最优路线(唯一的区别是最后一行)。
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 8 6 4
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 1 2 3
2 2
9 10 9 101 2 3 4 4 5
16
1 2 1 5 4 5
11
1 1
19思路
从第一列走到最后一列, 每个点有三个决策, 求最小权值和。 环形的处理就用取模运算, 或者递推时直接判断即可。
状态表示: f[i][j] 走到第 i 行, 第 j 列的点, 到达最右端还需要加上的最小权值。
状态计算:
f[i][j] = min(f[i + 1][j] + a[i][j], f[i][j])
f[i][j] = min(f[i + 1][j + 1] + a[i][j], f[i][j]) if j+1>m j=1
f[i][j] = min(f[i + 1][j - 1] + a[i][j], f[i][j]) if j-1<1 j=m
边界条件:f[n][j] = a[n][j]
代码
const int N = 110;
int a[N][N];
int f[N][N];
int nxt[N][N];
int n, m;
int main()
{
while(cin >> n >> m)
{
REPe(i, 1, n)
{
REPe(j, 1, m)
{
cin >> a[i][j];
}
}
mem(nxt, 0);
mem(f,0);
int res = 0x3f3f3f3f, first;
neREP(j, m, 1)
{
REPe(i, 1, n)
{
if (j == m)
f[i][j] = a[i][j];
else
{
int rows[3] = {i, i - 1, i + 1};
if (i == 1)
rows[1] = n;
if (i == n)
rows[2] = 1;
sort(rows, rows + 3);
f[i][j] = 0x3f3f3f3f;
REPe(k, 0, 2)
{
int v = f[rows[k]][j + 1] + a[i][j];
if (v < f[i][j])
{
f[i][j] = v;
nxt[i][j] = rows[k];
}
}
}
if (j == 1 && f[i][j] < res)
{
res = f[i][j];
first = i;
}
}
}
cout << first;
for (int i = nxt[first][1], j = 2; j <= m; i = nxt[i][j], j++)
cout << " " << i;
cout << "\n" << res << "\n";
}
return 0;
}9.3.2 0-1背包问题
完全背包
物品无限的背包问题。有n种物品,每种均有无穷多个。第i种物品的体积为Vi,重量 为Wi。选一些物品装到一个容量为C的背包中,使得背包内物品在总体积不超过C的前提下 重量尽量大。1≤n≤100,1≤Vi ≤C≤10000,1≤Wi≤106。
很像9.2节中的硬币问题,只不过“面值之和恰好为S”改成了“体积 之和不超过C”,另外增加了一个新的属性——重量,相当于把原来的无权图改成了带权图 (weighted graph)。这样,问题就变为了求以C为起点(终点任意)的、边权之和最大的路 径。 与前面相比,DAG从“无权”变成了“带权”,但这并没有带来任何困难,此时只需将某处 代码从“+1”变成“+W[i]”即可
例题9-5 劲歌金曲(Jin Ge Jin Qu [h]ao, Rujia Liu’s Present 6, UVa 12563)
dp 二维dp 01背包 如果问一个麦霸:“你在KTV里必唱的曲目有哪些?”得到的答案通常都会包含一首“神曲”:古巨基的《劲歌金曲》。
为什么呢?一般来说,KTV不会在“时间到”的时候鲁莽地把正在唱的歌切掉,而是会等它放完。例如,在还有 秒时再唱一首 分钟的歌,则实际上多唱了 秒。但是融合了 首歌曲的《劲歌金曲》长达 分 秒(5),如果唱这首,相当于多唱了秒!
假定你正在唱KTV,还剩 秒时间。你决定接下来只唱你最爱的 首歌(不含《劲歌金曲》)中的一些,在时间结束之前再唱一个《劲歌金曲》,使得唱的总曲目尽量多(包含《劲歌金曲》),在此前提下尽量晚的离开KTV。
输入和每首歌的长度(保证不超过 分钟),输出唱的总曲目以及时间总长度。输入保证所有 首曲子的总长度严格大于 。
Sample Input
2
3 100
60 70 80
3 100
30 69 70Sample Output
Case 1: 2 758
Case 2: 3 777思路
求能唱的数量最多, 且最多时求时间最长的, 显然是二维DP和这题很像 宠物小精灵之收服。
因为最后肯定是留至少1秒点金曲是最优, 故这里直接把输入的t减去1, 输出时判断一下, 如果是-1说明一个都点不了, 都输出0, 否则就在输出时把金曲加上。
其他就是正常的01背包了。
先求数量最多的, 然后逆序遍历求用时最多的。
滚动数组优化
状态表示: f[j] 恰好用时为j的最优选法
状态计算: f[j] = max(f[j], f[j - t] + 1)
注意全初始化为 -0x3f 负无穷, 因为这里求的是恰好为j。
题目给的t最大是1e9, 但实际上用不到这么多, 题目有说一首歌最多3分钟, 故总时间最大也就 180*n + 678。
代码
const int N = 55, T = 1e4 + 10;
int a[T];
int n, m;
int main()
{
int K;
cin >> K;
for (int kase = 1; kase <= K; kase++)
{
mem(a, -0x3f);
a[0] = 0;
cin >> n >> m;
m -= 1;
int res = 0;
for (int i = 1; i <= n; i++)
{
int t;
cin >> t;
for (int j = m; j >= t; j--)
{
a[j] = max(a[j], a[j - t] + 1);
}
}
for (int i = 0; i <= m; i++)
res = max(res, a[i]);
int time = 0;
for (int i = m; i >= 0; i--)
if (a[i] == res)
{
time = i;
break;
}
if (m != -1)
{
printf("Case %d: %d %d\n", kase, res + 1, time + 678);
}
else
printf("Case %d: %d %d\n", kase, 0, 0);
}
}