9.4.1 线性结构上的动态规划
例题9-6 照明系统设计(Lighting System Design, UVa 11400)
[[线性DP类#Lighting System Design | 之前写过]]
例题9-7 划分成回文串(Partitioning by Palindromes, UVa 11584)
dp 线性dp 字符串回文 输入一个由小写字母组成的字符串,要求把它划分成尽量少的回文串。输出最少的个数。 如aaadbccb最少可以划分为3个:aaa,d,bccb
输入: 第一行输入一个n表示数据组数 接下来n行每行输入一个字符串s(1⇐s⇐1000)
输出: 输出一个数表示最少的个数
input
3
aaadbccb
ffgcc
juzioutput
3
3
4`思路
状态表示: f[i] 是 1~i 中回文串个数
状态计算: f[i] = min(f[i], f[j] + 1 ) if i~j 是一个回文串
所以先用n^2把这个串中的所有回文字串标识出来。
枚举中心, 然后向左右延伸, 如果是不同就标识为false, 是的话就true
bool is_palindrome(int i, int j)
{
if(i >= j) return true;
if(s[i] != s[j]) return false;
if(st[i][j] == kase) return p[i][j];
st[i][j] = kase;
p[i][j] = is_palindrome(i+1,j-1);
return p[i][j];
}代码
const int N = 1e3 + 10;
例题9-8 颜色的长度(Color Length, ACM/ICPC Daejeon 2011, UVa1625)
输入两个长度分别为n和m(n,m≤5000)的颜色序列,要求按顺序合并成同一个序列, 即每次可以把一个序列开头的颜色放到新序列的尾部。 例如,两个颜色序列GBBY和YRRGB,至少有两种合并结果:GBYBRYRGB和 YRRGGBBYB。 对于每个颜色c来说,其跨度L(c)等于最大位置和最小位置之差。例如,对 于上面两种合并结果,每个颜色的L(c)和所有L(c)的总和如图所示。
你的任务是找一种合并方式,使得所有L(c)的总和最小
1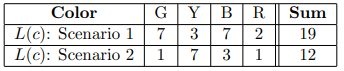
输入格式
第一行输入T组样例 每组包含两行: 第一行是长度为n的字符串 n (1 ≤ n ≤ 5, 000) 第二行是长度为m的字符串 m (1 ≤ m ≤ 5, 000) 每个颜色序列都是小写英文字母
输出格式
每组样例输出一行 合并后最小的L(c)总和
思路
设 f[i][j] 为移走了第一个序列前i个元素, 第二个序列前j个元素, 还需要多少费用。
指标函数:需要最小化的函数。
本题的指标函数比较复杂, 出现某种颜色时并不知道该颜色什么时候结束, 当某个颜色的最后一个元素合并之后, 又不知道它什么时候第一次出现。
如果记录每个颜色第一次出现的位置, 状态会很复杂, 枚举所用时间也很多。 所以只能换种方向, 在指标函数的计算方式上想办法:不是等到一个颜色全部移动完再算, 而是遇到时就累加。 换句话说,当把一个颜色移到最终序列前,需要把所有“已经出现但还没结束”的颜色的L(c)值加1。更进一步地,因为并不关心每个颜色的L(c),所以只需要知道有多少种颜色已经开始但尚未结束。
例如,序列GBBY和YRRGB,分别已经移走了1个和3个元素(例如,已经合并成了 YRRG)。下次再从序列2移走一个元素(即G)时,Y和G需要加1。下次再从序列1移走一个元素(它是B)时,只有Y需要加1(因为G已经结束)。
这样,可以事先算出每个颜色在两个序列中的开始和结束位置,就可以在动态规划时在O(1)时间内计算出状态d(i,j)中“有多少个颜色已经出现但尚未结束”,从而在O(1)时间内完成状态转移。
状态总是为O(nm)个,总时间复杂度也是O(nm)。
代码
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
int readInt()
{
int t;
cin >> t;
return t;
}
//------- Coding Area ---------//
const int N = 5e3 + 10, INF = 0x3f3f3f;
int sq[26], eq[26], sp[26], ep[26];
int f[2][N];
int c[2][N];
int n, m;
char q[N], p[N]; // start with 1 position
int main()
{
int T;
cin >> T;
while (T--)
{
scanf("%s%s", p + 1, q + 1);
n = strlen(p + 1);
m = strlen(q + 1);
//cout << p + 1 << " " << q + 1 << endl;
// cout << n << m << endl;
for (int i = 1; i <= n; i++)
p[i] -= 'A';
for (int i = 1; i <= m; i++)
q[i] -= 'A';
for (int i = 0; i < 26; i++)
{
sq[i] = sp[i] = INF;
eq[i] = ep[i] = 0;
}
for (int i = 1; i <= n; i++)
{
sp[p[i]] = min(sp[p[i]], i);
ep[p[i]] = i;
}
for (int i = 1; i <= m; i++)
{
sq[q[i]] = min(sq[q[i]], i);
eq[q[i]] = i;
}
mem(c, 0);
mem(f, 0);
int t = 0;
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= m; j++)
{
if (!i && !j)
continue;
int v1 = INF, v2 = INF;
if (i)
v1 = f[t ^ 1][j] + c[t ^ 1][j];
if (j)
v2 = f[t][j - 1] + c[t][j - 1];
f[t][j] = min(v1, v2);
if (i)
{
c[t][j] = c[t ^ 1][j];
if (sp[p[i]] == i && sq[p[i]] > j)
c[t][j]++;
if (ep[p[i]] == i && eq[p[i]] <= j)
c[t][j]--;
}
else if (j)
{
c[t][j] = c[t][j - 1];
if (sq[q[j]] == j && sp[q[j]] > i)
c[t][j]++;
if (eq[q[j]] == j && ep[q[j]] <= i)
c[t][j]--;
}
}
t ^= 1;
}
cout << f[t ^ 1][m] << endl;
}
return 0 ;
}最优矩阵链乘
区间dp 线性dp 最优矩阵链乘。一个n×m矩阵由n行m列共个数排列而成。两个矩阵A和B可以相乘当且仅当A的列数等于B的行数。一个n×m的矩阵乘以一个m×p的矩阵等于一个的矩阵,运算量为mnp。
矩阵乘法不满足分配律,但满足结合律,因此A×B×C既可以按顺序(A×B)×C进行,也可以按A×(B×C)进行。假设A、B、C分别是2×3,3×4和4×5的,则(A×B)×C的运算量为2×3×4+2×4×5=64,A×(B×C)的运算量为3×4×5+2×3×5=90。显然第一种顺序节省运算量。
给出n个矩阵组成的序列,设计一种方法把它们依次乘起来,使得总的运算量尽量小。假设第i个矩阵Ai是的。
思路
划分最优子结构, 有最后一次乘法, 假设为k个乘号, 那么在此之前就已经算出
P = A1 * A2 * A3 * ... * Ak 和 Q = Ak+1 * Ak+2 * Ak+3 * ... * An
因为 P 和 Q 的计算过程互不影响, 且无论怎么算 P Q 的值都不会变化, 所以只需分别让PQ按照最优方案计算即可。
计算P和Q时还需要继续拆分。
子问题合并:计算 Aij = 计算Aik + 计算Akj + Ai-1k * Ai
故子问题为:把Ai, Ai+1, ... , Aj 乘起来需要多少次乘法
状态表示: f[i][j] 把 Ai - Aj 乘起来的最小乘法数量
状态计算: f[i][j] = min(f[i][j], f[i][k] + f[k][j] + pi-1*pk*pj)
初始化为 f[i][i] = 0
递推顺序为
代码
例题9-9 切木棍(Cutting Sticks, UVa 10003)
有一根长度为的棍子, 还有个切割点的位置(按照从小到大排列)。你的任务是在这些切割点的位置处把棍子切成部分, 使得总切割费用最小。每次切割的费用等于被切割的木棍长度。例如, , 切割点为。如果按照的顺序, 费用为, 如果按照的顺序, 费用为。
输入多组数据。 每个测试用例的第一行将包含一个正数l, 它表示要切割的木棍的长度。。 下一行将包含的切割次数。 下一行由个正数组成, 表示必须进行切割的位置, 按照严格递增的顺序给出。 的输入情况表示输入的结束。 Output 输出切割问题最优解的成本, 也就是切割给定棒的最小成本。 如下所示格式化输出。
Sample Input
100
3
25 50 75
10
44 5 7 8
0Sample Output
The minimum cutting is 200.
The minimum cutting is 22.思路
若没给定切割点, 则可以直接区间DP整个长度, 这里给定切割点则需要根据切割点来进行DP。
根据切割点枚举的话, 切割点之间很好计算, 比如:
有切割点 2 4 7, 代表位置在[2,7]长度为5的木棍, 可以用中间的切割点。
状态表示: f[i][j] 位置在(i,j)的小木棍切割后的最小成本
状态计算: f[i][j] = min(f[i][k] + f[k][j] + a[j] - a[i]) 其中 i < k < j
第一刀如何保证加上总长度呢?
可以让 a[0], a[n + 1]代表总长度, 从[0,n+1]开始计算。
起始条件为len == 2, f[i][j] = 0
最终结果为f[0][n+1]
代码
const int N = 1e3 + 10;
int f[N][N];
int a[N];
int n;
int main()
{
int l;
while (cin >> l && l)
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + 1 + n);
a[0] = 0, a[n + 1] = l;
memset(f, 0x3f, sizeof f);
for (int len = 2; len <= n + 2; len++)
{
for (int i = 0; i + len - 1 <= n + 1; i++)
{
int j = i + len - 1;
if (len == 2)
f[i][j] = 0;
else
{
for (int k = i + 1; k < j; k++)
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + a[j] - a[i]);
}
}
}
cout << "The minimum cutting is " << f[0][n + 1] << ".\n";
}
return 0;
}例题9-10 括号序列(Brackets Sequence, NEERC 2001, UVa1626)
定义如下正规括号序列(字符串): 空序列是正规括号序列。 如果是正规括号序列, 那么和也是正规括号序列。 如果和都是正规括号序列, 那么也是正规括号序列。
例如, 下面的字符串都是正规括号序列:(), [], (()), ([]), ()[], ()[()], 而如下字符串则不是正规括号序列:(, [, ], )(, ([()。
输入一个长度不超过的, 由(, ), [, ]构成的序列, 添加尽量少的括号, 得到一个规则序列。如有多解, 输出任意一个序列即可。
样例
1
([(]
()[()]思路
假设串S至少要添加个括号, 转移如下:
- 如果形如 或者, 转移到
- 如果至少有两个字符, 则可以分成, 转移到
边界是: 为空时, 为单字符时。
状态表示: f[i][j] 字串至少需要添加几个括号, 其中为空的字串用f[i+1][i]表示, 单字符的字串用f[i][i]表示
状态计算:
f[i][j] = min(f[i][k] + f[k + 1][j]) k in[i,j)
and f[i][j] = min(f[i+1][j-1]) if match(s[i],s[j])