区间选点
给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 N，表示区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。
输出格式
输出一个整数，表示所需的点的最小数量。
数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
思路
只有当一个区间与另一个区间重叠时, 两个区间可以只选择一个点。
故我们只需要找最小的那个区间就行。
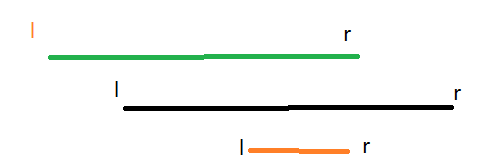遍历到绿色区间时, 需要一个点。
遍历到黑色区间时, 因为与绿色区间重叠, 故不需要增加点
遍历的橘色区间时, 同样 重叠, 不增加新点
怎么判断与上一个区间重叠？
记录上一个区间的 L, R
若当前区间的 l > R, 则说明没有重叠, cnt++, 更新 L, R 为当前区间
若当前区间的 l <= R, 则说明重叠, 不必cnt++, 但需要将 R 更新为 较小值
因为判断后面的是否重叠跟最小的R有关
代码
#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
typedef pair<int,int> PII;
PII s[N];
int n;
int main()
{
cin >> n;
for(int i = 0; i < n;i ++)
{
int a,b;
cin >> a >> b;
s[i] = {a,b};
}
sort(s, s + n);
int cnt = 0, L = -2e9, R = -2e9;
for(int i = 0; i < n;i ++)
{
int l = s[i].first, r = s[i].second;
if(l > R)
{
cnt++;
L = l, R = r;
}
else R = min(R, r);
}
cout << cnt << endl;
return 0;
}区间分组
给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数 N，表示区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。
输出格式
输出一个整数，表示最小组数。
数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
思路
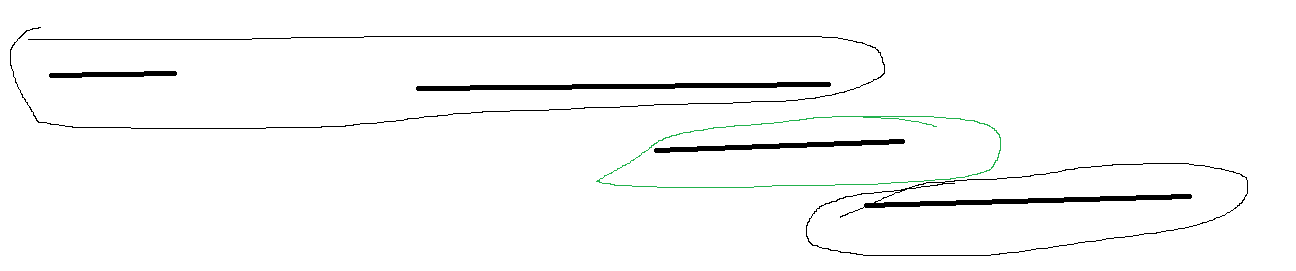分两组, 当该区间的左端点小于之前分组中最大右端点时重合, 分到新组里。
对所有区间根据左端点进行排序, 这样中间不会有空隙。
对于区间i, 当 i.l 小于等于 所有分组中最小的那个 max_r, 就肯定与所有分组重叠, 需要新增一个分组。 若大于则说明 可以加入到 最小的那个分组里, 如果 i.r 大于 max_r 则更新 一下。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
struct Range{
int l, r;
}range[N];
int n;
struct cmpFunctor{
inline bool operator () (const Range &a, const Range &b)
{
return a.l < b.l;
}
};
int main()
{
cin >> n;
for(int i = 0; i < n; i++)
{
int l,r;
cin >> l >> r;
range[i] = {l,r};
}
sort(range, range + n,cmpFunctor());
priority_queue<int, vector<int>, greater<int>> q;
for(int i = 0; i < n; i++)
{
if(q.empty() || q.top() >= range[i].l)
q.push(range[i].r);
else
{
q.pop();
q.push(range[i].r);
}
}
cout << q.size() << endl;
return 0;
}区间覆盖
给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。
输出最少区间数，如果无法完全覆盖则输出 −1。
输入格式
第一行包含两个整数 s 和 t，表示给定线段区间的两个端点。
第二行包含整数 N，表示给定区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。
输出格式
输出一个整数，表示所需最少区间数。 如果无解，则输出 −1。
数据范围
1≤N≤105,
−109≤ai≤bi≤109,
−109≤s≤t≤109
输入样例：
1 5
3
-1 3
2 4
3 5
输出样例：
2
思路
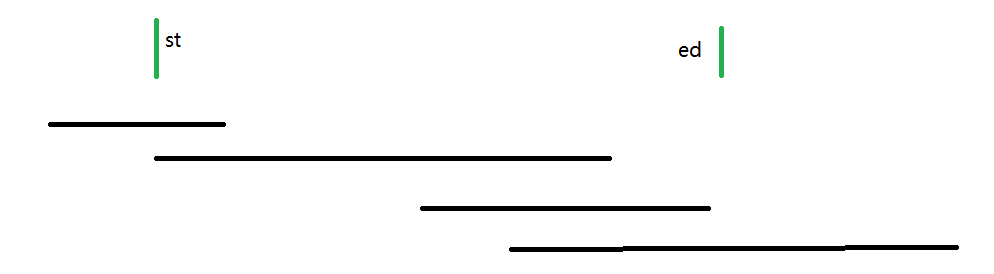用第二个和第四个最好。
对于 i.l <= st 的区间, 选择右端点最大的 max_r
然后将右端点重置为 st, 接着重复选择。
当 max_r 始终小于 ed 时, 说明无法覆盖, 若超过ed则直接退出提交答案
故按左端点排序, 遍历所有区间
从i开始, 往后找最后一个 range[i].l <= st 的区间, 期间一直更新 max_r
判断 max_r 是否小于 st, 若小于说明没有区间能覆盖开头
判断 max_r 是否大于 ed, 若大于说明已经覆盖结尾
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
struct Range{
int l, r;
}range[N];
int n;
int s,t;
struct cmpFunction
{
inline bool operator () (const Range&a, const Range&b)
{
return a.l < b.l;
}
};
int main()
{
cin >> s >> t >> n;
for(int i = 0; i < n;i ++)
{
int l,r;
cin >> l >> r;
range[i] = {l,r};
}
sort(range, range + n, cmpFunction());
int res = 0;
bool flag = false;
for(int i = 0; i < n;i ++)
{
int j = i, r = -2e9;
while(j < n && range[j].l <= s)
{
r = max(r, range[j].r);
j++;
}
if(r < s)
{
res = -1;
break;
}
res++;
if(r >= t)
{
flag = true;
break;
}
s = r;
i = j - 1;
}
if(!flag) res = - 1;
cout << res << endl;
return 0;
}