绝对值不等式 中点最小

货仓选址

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式

第一行输入整数 N。

第二行 N 个整数 A1∼AN。

输出格式

输出一个整数，表示距离之和的最小值。

数据范围

1≤N≤100000,
0≤Ai≤40000

输入样例：

4
6 2 9 1

输出样例：

12

思路

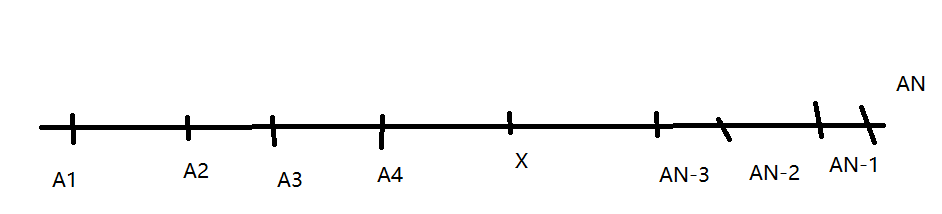
求x的位置, 满足所有点与x的距离差和最小。 列出式子：

\begin{eqnarray}
f(x) & = & |a_1 - x| + |a_2 - x| + |a_3 - x| ... |a_{n-3} - x|+ |a_{n-2}-x| +|a_{n-1}-x| + |a_n - x| 
\end{eqnarray}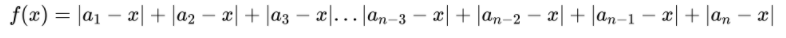

显然, 可以让每一项都成为最小的, 和就是最小的。

先拿出 a1, a2, 看x选哪个点是让 第一第二项最小: 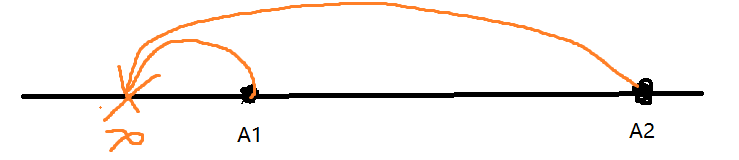若x在两点的左边, 则为 2*A1 + A2, 右边同理 显然在 A1 和 A2 之间最短, 最短时为中点。

同理来说, 其他所有点的差也是如此, 在 A1 和 An 之间, 肯定有一个点是最小点。 所以当 A1 <= x <= An 时, f(x) >= 最小值, 什么时候取到等号呢？

两个点时是中点, 为何不猜多个数时也是中位数呢。 即 x = A[n / 2 + 1](sort后)

代码

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1e5 +10;
int n;
int a[N];
 
int main()
{
    cin >> n;
    for(int i = 1; i <= n;i ++) scanf("%d", &a[i]);
    sort(a + 1, a + n + 1);
    int mid = a[n / 2 + 1], res = 0;
    for(int i = 1; i <= n; i++) res += abs(a[i] - mid);
    cout << res << endl;
    return 0;
}