🪴 Edwin Aze's Blog

最近文章

最近笔记

中国剩余定理

10分钟阅读

模板

互质版本

作用： 求 n 组线性同余方程的通解

非互质

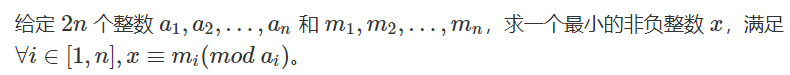
可以转化为 x = k*a + m 先写两个线性同余方程组的解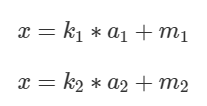： 等式两边相等得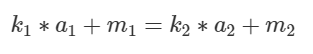： 移项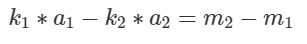： 格式类似于扩展欧几里得定理, 整理一下：

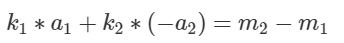
显然, 如果 m2- m1 是 gcd(a1, -a2) 的倍数, 则始终可以找到 k1, k2 使得等式成立

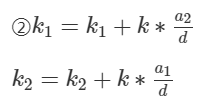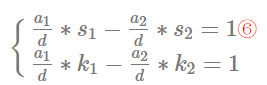k1*a1 - k2*a2 = b2 - b1; 由于扩展欧几里得定理： 当 b2-b1 是 a1,a2 最小公约数的倍数时, 使用exgcd可以得出k1,k2 即 LL d = exgcd(a1, -a2, k1, k2); 因为模数运算的性质, 这里k1有可能是负数, 进行扩大 k1 = k1 * (b2 - b1) / d; (x = x * b / d) LL t = a2 / d; 转为通解 k1 = (k1 % t + t) % t; 把特解变成通解： 证明： 同除以d 相减

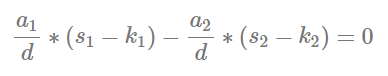
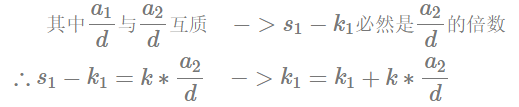转化为 在方程组6中根据裴蜀定理的推论(a,b互质的充要条件是存在整数x,y使ax+by=1)从而得出它两互质

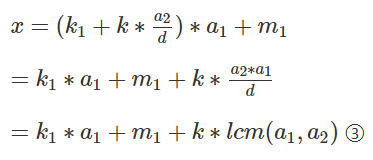
故 x 可化为： 这样就得到x的有关a1, a2的通解, 接下来继续合并剩下的式子, 求最小解即可。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
 
LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL t = exgcd(b, a % b, y, x);
    y -= a/b * x;
    return t;
}
 
 
int n;
int main()
{
    cin >> n;
    LL a1, m1;
    cin >> a1 >> m1;
    bool flag = true;
    n-=1;
    while (n -- ){
        LL a2, m2;
        LL k1, k2;
        cin >> a2 >> m2;
        LL d = exgcd(a1, -a2, k1, k2);
        if((m2 - m1) % d)
        {
            flag = false;
            break;
        }
        k1 *= (m2-m1)/d; // 扩大
        LL t = a2 / d;
        k1 = (k1 % t + t) % t; // 变成正数,且为最小解
        m1 = k1*a1 + m1;
        a1 = abs(a1/d*a2);
    }
    if(flag) cout << (m1 % a1 + a1) % a1 << endl;
    else cout << -1 << endl;
    return 0;
}

X问题

求在小于等于N的正整数中有多少个X满足：

X mod a[0] = b[0], 
X mod a[1] = b[1], 
X mod a[2] = b[2],
…, 
X mod a[i] = b[i],
… 
(0 < a[i] <= 10)。

思路

跟中国剩余定理一样的结构, 那么就转化一下： x = k1*a[0] + b[0] x = k2 * a[1] + b[1] 先看前两个式子如何合并: k1*a[0] + b[0] = k2 * a[1] + b[1] 移项得： k1 * a[0] - k2 * a[1] = b[1] - b[0] 因为正负无所谓, 所以这里直接把 a[1] 变成负数 k1 * a[0] + k2 * a[1] = b[1] - b[0] 通过扩展欧几里得定理得出 k1, k2 的值, 然后化为通解 k1 = k1 + k*(a[1] / d) k2 = k2 + k*(a[0] / d) 带入x中得： x = (k1 + k * a[1] / d)*a[0] + b[0] x = k * (a[1] / d) * a[0] + k1*a[0] + b[0] 故合并后x的式子中： a 为 k * (a[1] / d) * a[0] b 为 k1 * a[0] +b[0] 则更新时这样更新：

b1 = k1 * a1 + b1;
a1 = abs((a1 / d) * a[i]); // a1 一般比 a[i] 大, 故防溢出先除 a1

最后的答案 x = b1 + k*a1 其中 b1 就是最小的x, 求在N之下有多少个x成立, 则将 k 变成1, 2, 3 … 直到 x 超出n即可。

根据扩展欧几里得定理可得, 当 b[1] - b[0] 无法被 gcd(a1, a[i]) 整除时, 无法合并, 无解。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
inline int readInt()
{
    int t;
    scanf("%d", &t);
    return t;
}
template <typename T>
inline T exgcd(T a, T b, T &x, T &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    T t = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return t;
}
//------- Coding Area ---------//
const int N = 1e2 + 10, MOD = 100003;
// int f[N][N];
long long n, m;
long long a[12], b[12];
int main()
{
    int T;
    cin >> T;
    while (T--)
    {
        cin >> n >> m;
        for(int i = 0; i < m; i++) a[i] = readInt();
        for(int i = 0; i < m; i++) b[i] = readInt();
        long long a1 = a[0], b1 = b[0], k1, k2;
        bool flag = true;
        for(int i = 1; i < m; i++)
        {
            long long d = exgcd(a1, -a[i], k1, k2);
            if ((b[i] - b1) % d)
                flag = false;
            // 这里是优化为最小整数解, 提高速度
            k1 *= (b[i] - b1) / d;
            long long t = a[i] / d;
            k1 = (k1 % t + t) % t;
            
            b1 = k1 * a1 + b1;
            a1 = abs((a1 / d) * a[i]);
        }
        if (flag && b1 <= n)
        {
            b1 = (b1 % a1 + a1) % a1;
            long long res = (n - b1) / a1; // 这是除去 最小非负整数x 之后的其他解
            if (b1 != 0 && b1 <= n) // 若 x 不为0则算一个解
                res++;
            cout << res << endl;
        }
        else
            cout << 0 << endl;
    }
    return 0;
}

Hello Kiki

title: 题目
One day I was shopping in the supermarket. There was a cashier counting coins seriously when a little kid running and singing "门前大桥下游过一群鸭，快来快来 数一数，二四六七八". And then the cashier put the counted coins back morosely and count again...  
Hello Kiki is such a lovely girl that she loves doing counting in a different way. For example, when she is counting X coins, she count them N times. Each time she divide the coins into several same sized groups and write down the group size Mi and the number of the remaining coins Ai on her note.  
One day Kiki's father found her note and he wanted to know how much coins Kiki was counting.
 
title: input
2
2
14 57
5 56
5
19 54 40 24 80
11 2 36 20 76
title: output
Case 1: 341
Case 2: 5996
 
title: 思路
 
简单做下英语阅读可得, 该题要求你找到硬币总数X, 满足分k次,每次分出来Mi个, 最后剩下Ai个。
转化为数学表达：
$$x \equiv A_{i}(mod M_{i}) $$
显然, 是中国剩余定理的模板题。
套用即可, 求出所有式子中 x 的通解：
 
$$
\begin{gather*}
 
x = k_{1}*M_{1} + A_{1} \\
x = k_{2}*M_{2} + A_{2} \\
k_{1}*M_{1} + A_{1} = k_{2}*M_{2} + A_{1}\\
k_{1}*M_{1} - k_{2}*M_{2} = A_{1} - A_{2} \\
根据 扩展欧几里得定理 得, 当 (A_{1}-A_{2}) 是 gcd(M_{1}, M_{2}) 的倍数时, 有无数个 k_{1}, k_{2}解
\end{gather*}
$$
由此可以求得 x 的特解, 将其转化为通解得：
$$k_{1} = k_{1} + k * \frac{M_{2}}{gcd(M_{1}, M_{2})}$$
然后代回 x, 即是 x 的通解表达：
$$x = k*lcm(M_{1}, M_{2}) + [k_{1} * M_{1} + A_{1}]$$
括号中是x的最小解（可以为负数也可以为0）, k为任意正整数, 将k增加即可获得更大的解。
这是合并第一第二个式子, 之后把其他式子按同样模式合并即可。
 
#include <iostream>
#include <algorithm>
using namespace std;
 
template <typename T>
inline T exgcd(T a, T b, T &x, T &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    T t = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return t;
}
//------- Coding Area ---------//
const int N = 1e2 + 10;
typedef long long LL;
LL a[N], b[N];
 
int main()
{
 
    int T;
    cin >> T;
    int cnt = 0;
    while (T--)
    {
        LL n, a1, b1;
        cin >> n;
	    for(int i = 0; i < n;i ++) cin >> a[i];
        for(int i = 0; i < n;i ++) cin >> b[i];
        a1 = a[0], b1 = b[0];
        bool flag = true;
        for(int i = 1; i < n; i++)
        {
            LL k1, k2;
            LL d = exgcd(a1, -a[i], k1, k2);
            LL lcm = a1 / d * a[i];
            if ((b[i] - b1) % d) // 若不满足定理使用条件说明无解
                flag = false;
            k1 *= (b[i] - b1) / d; // 扩大
            LL t = a[i] / d;
            k1 = (k1 % t + t) % t; // 保证为最小解
            b1 = k1 * a1 + b1; // 更新
            a1 = abs(lcm);
        }
        if (!flag)
            cout << "Case " << ++cnt << ": " << -1 << endl;
        else if (b1 != 0)
            cout << "Case " << ++cnt << ": " << (b1 % a1 + a1) % a1 << endl;
        else // 0不能算结果哦
            cout << "Case " << ++cnt << ": " << b1 + a1 << endl;
    }
 
    return 0;
}

反向链接